右の図の赤い三角形に, 外角の定理を使う。 ア=34+77 =111(度)。 下の図の赤い三角形に外角の定理を利用して, z=50+36=86(度)。 wの角度は,180-(86+44)=50(度)だから, 青い三角形に外角の定理を利用して,三角形の角度の合計の定理 定理によると、ユークリッド平面上にある特定の幾何学図形のすべての角を合計すると、その合計は180度になります。 この定理を証明してみましょう。 KMNの頂点を持つ任意の三角形を作りましょう。 頂点Mを通して、直線KNに平行な直線を描きます(この直線はユークリッド直線とも呼ばれます)。 点KとAが直線MNの異なる側に位置する印をつけた角の和 三角形の1つの外角はそれと隣り合わない2つの内角の和に等しい a b x ∠x=∠a∠bである。 abcdeの値を求めよ。 a c b d e a c b d e ac bd 赤い三角形に着目して内角と外角の関係から、図に示した角がacになる。 >> ac
失踪的正方形 维基百科 自由的百科全书
三角形 角度 合計
三角形 角度 合計- 三角形の角度 よっしーオンライン家庭教師の中学数学の解説 Noschool 角度の問題まとめ 中学入試算数 よく出る問題はこれ 角度の合計は 浅野中学 031 定理を理解する 余弦(コサイン)定理を理解しておくと、いかなる三角形でも2つの辺の長さと、その間の角度が分かっていれば外周を算出することができます。 この法則はどのような三角形でも当てはめることができ、とても便利です。 余弦定理によれば、3つの辺 a 、 b 、そして c と、それぞれの辺と向かい合った角度 A 、 B 、 C がある場合、 c2 = a2 b2 2ab cos



直角三角形角度計算公式 直角三角形角度計算公式線上資訊以及角度計app認知角度計app 共68筆1 1頁 App開箱王
小学校5年生で習う「三角形の内角の角度」 を求める問題集です。 問題をランダムで生成することができ、答えの表示・非表示も切り替えられます。印刷してご活用ください。 ちなみに三角形の内角の角度の求め方についてはこちらに詳しく説明しています。角度3 解説 三角形の外角は それと隣り合わない2つの内角の和に等しい。 m n mn 補助線の引き方。 1三角形をつくる (内角の和または外角の関係を使う) 2 平行線をひく (錯角、または同位角を使う) 1 m//nのとき次のxの値を求めよ。 (1) m n x 100° ° 70° (2) m 小学校のとき三角形はどんな形でも角の合計が180度だと習ったと思いますが、 大人になってふとその理由が気になりました。 四角形も角の合計が360度になりますが、 180度=半円の角度、360度=円1周の角度との関連はあるのでしょうか?
直角三角形の選択した2つの入力値から他の要素の値を計算します 使用目的 教科書の直角三角形の角度計算 ご意見・ご感想 小学生の教科書は、結論を導く過程で、整数ではない角度をはかって確かめさせるような場合があるので、助かります 三角形の角度測定値を見つける方法 三角形の3つの从已知两边求角度 若我们知道 直角三角形 两条边的长度,我们便可以求三角形的未知角度。 例子 梯子搁在墙上,如图。 梯子与墙之间的 角度 是多少?三角形の内角の和が180度であることを、幼稚園児でも理解できるように折り紙を使って証明する方法を紹介します 誰もが一度は見たことがある方法かもしれませんが、ほとんどの大人は忘れ なぜ三角形の角度の合計は180度なんでしょう? するともともと三角形の各、内角が一箇所に
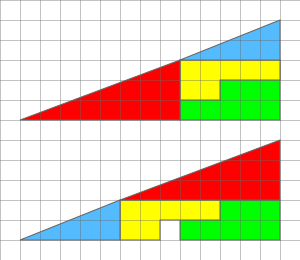
ぜいたく 三角形 角度 合計 三角形底部形态该如何操作 股市三角形的操作小技巧 上升三角形 零点财经 三角形の内角の和 Youtube 三角形の内角の和 算数の公式覚えてますか 三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun 三角形の内角 内容は単純で、以下の三角形の角度合計を求めるだけです。 結構有名な問題らしくて、補助線を使えば簡単に求めることができるとのことでしたので、考えてみました。 以下の画像の問題で、同じ大きさの正方形が3個横に繋がっており、一番左の正方形の角から、他の正方形の角まで伸びた線がなす角の合計を求めるものです。 具体的には、以下の図のα三角形(さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。 その3点を三角形の頂点、3つの線分を三角形の辺という。




U3bnbzudjbtrjm




角度を計算する方法 9 ステップ 画像あり Wikihow
(1)角ABCは経線と緯線が垂直に交わる地点なので角度は90度。 (2)角CBAは経線と緯線が垂直に交わる地点なので角度は90度。 (3)角BACは頭上から見ると球体を4分割するので角度は90度。 よって三角ABCの内角の和は270°になります。二等辺三角形の角度は? 二等辺三角形の角度は、1つの角度が分かれば、他の2つの角度が計算できます。下図をみてください。これが二等辺三角形です。 三角形の角度は合計すると180度です。頂角をα、低角をθとします。よって α2θ=180 です。角度がまとめられれて、 しかもそれが一直線上にあれば求めるのは簡単です。 一直線の角度とは、すなわち180度ですからね。 したがって 三角形の内角の和=180度 となるのです。



Tableau雷达图制作 这可能是你能看到最详尽 最清爽 最感人的教程 码农家园




多規格可選 夕米筆記本電腦支架托架散熱桌面增高底座升降便攜式頸椎懸空架子筆電架電腦架筆電懶人支架筆電散熱架散熱
先端に三角形が5つある ので内角の和の合計は180° きる五角形の外角の和は 360°でそれが2つ分なの -7=180°になります。 三角形の2つの内角の和の c+e はfにき て、b+dはgにくる。する と、上の三角形の内角に集ま ってくるから180°になりま す。180°×2=360° となった。 五角形の場合も同じように考えると、 3 つの三角形がで きるので、内角の和は 180°×3=540° 六角形の内角の和は、 180°×4=7° n 角形の場合を考えると、一つの頂点から対角線を引い てできる三角形の数はS formula (1) S =√s(s−a)(s−b)(s−c), s = (abc) 2 (2) if a≥b,c h = 2S a, B=sin−1 h c, C= sin−1 h b if b≥ c,a h = 2S b, C =sin−1 h a, A=sin−1 h c if c≥ a,b h = 2S c, A= sin−1 h b, B=sin−1 h a (3) ABC
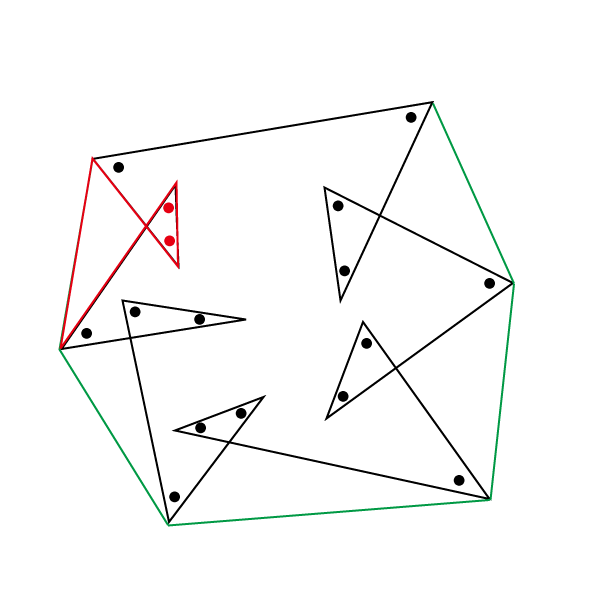



角度情報がない図形の合計の角度 星形多角形 受験算数入門



主流航司机场年年报图鉴 整体亏损超千亿机场商业生意受重创 每日经济新闻
多角形の内角の角度の合計を見つける 角度の合計を求めるには、 (n – 2) x 180という計算式を用います。 ここでの「n」とは多角形を構成する辺の数を意味しています。 また、最も一般的な多角形の角度の合計は下記の様になっています。 三角形(3辺から三角形をかいて、分度器で角度をはかり、合計するという方法以外に、写真のようなたしかめ方もあります。 ①三角形をかいて、3つの角に印をつける。 ②三角形を切り取る。 ③3つの角が残るように、三角形を切る。 ④3つの角を集めて並べる。・直角三角形(底辺と角度) 直角三角形の底辺と角度から、高さと斜辺と面積を計算します。 ・直角三角形(高さと斜辺) 直角三角形の高さと斜辺から、底辺と角度と面積を計算します。



Www Unpri Org Download Ac 2962




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
今回は、三角形の角度を求める問題を解いていきたいと思います。 三角形の内角の和は180° 三角形の外角の大きさ=となり合わない2つの内角の和 三角形の角度を求める問題 問題① 問題② 問題③ 問題④ 三角形の角度を求める問題では、対頂角・同位角・錯角の性質や二等辺三角形の性質四角形の性質 直線図形 (入試問題) → スg スム版は別包ソス スy スd スv ス ス ス ス スz ス 剳モ三 スp ス` スフ暦ソス ス スp スヘ難ソス ス ス ス ス スD ス@ スE ス} スP スフ三 スp ス` ABC ス ス AB=AC スフ二等辺三 スp ス` スネゑソス ス ス ス ABC= ス ス ACBトライアングル電卓 November31 ツール 全ユーザー対象 5,634 広告を含む ほしいものリストに追加 三角法で使用されるように残りの値を見つけるには2つの側面と1角、2角と片側または三辺を入力して三角形を解く。 角度は分と秒と度、ラジアン、グラード



Http Rportal Lib Ntnu Edu Tw Bitstream 500 1 s01 Pdf




亚洲市场自保态度 Willis Towers Watson
三角形や四角形と同様に考えると、n角形の 外角 の和も同じ 360 ∘ です。三角形の内角の和が180度なのは知っていますよね? その三角形が2個あります。 つまり、 三角形1と三角形2の内角の和の合計が 四角形の内角の和 になるということ。したがって 四角形の内角の和=360度 となるのです。すべての三角形の内角の合計は常に= 180になります : 二等辺三角形では、底辺の角度は常に合同です。つまり、それらは同じ尺度を持ちます。 = Ê= 55 角度の値を決定するにはÊ最初のルールの他の角度の値を代入してクリアします。Ê: 55 55 ≈= 180




重磅 李佳琦 薇娅都准备携自家公司上市 全网搜




小5 算数 小5 31 三角形の角 Youtube
動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → http//19chtv/ Twitter→ https//twittercom/haichi_toaru三角形にはいろんな種類があり、形や大きさは様々です。 しかしどんな三角形でも、 「3 3 つの角の内角をすべて足すと絶対に180° 180 ° になる」 という定理があります。 「図の a a の角度を求めよ」というような問題が出された場合にこれを用います。二等辺三角形の両底角は等しい. が成り立ちます. この性質と三角形の内角の和が 180 °になるという性質を使うと,二等辺三角形の3つの角のうち1つの角が分かれば,残りの角が求められます. 例1 頂角が与えられている問題 が成り立ちます
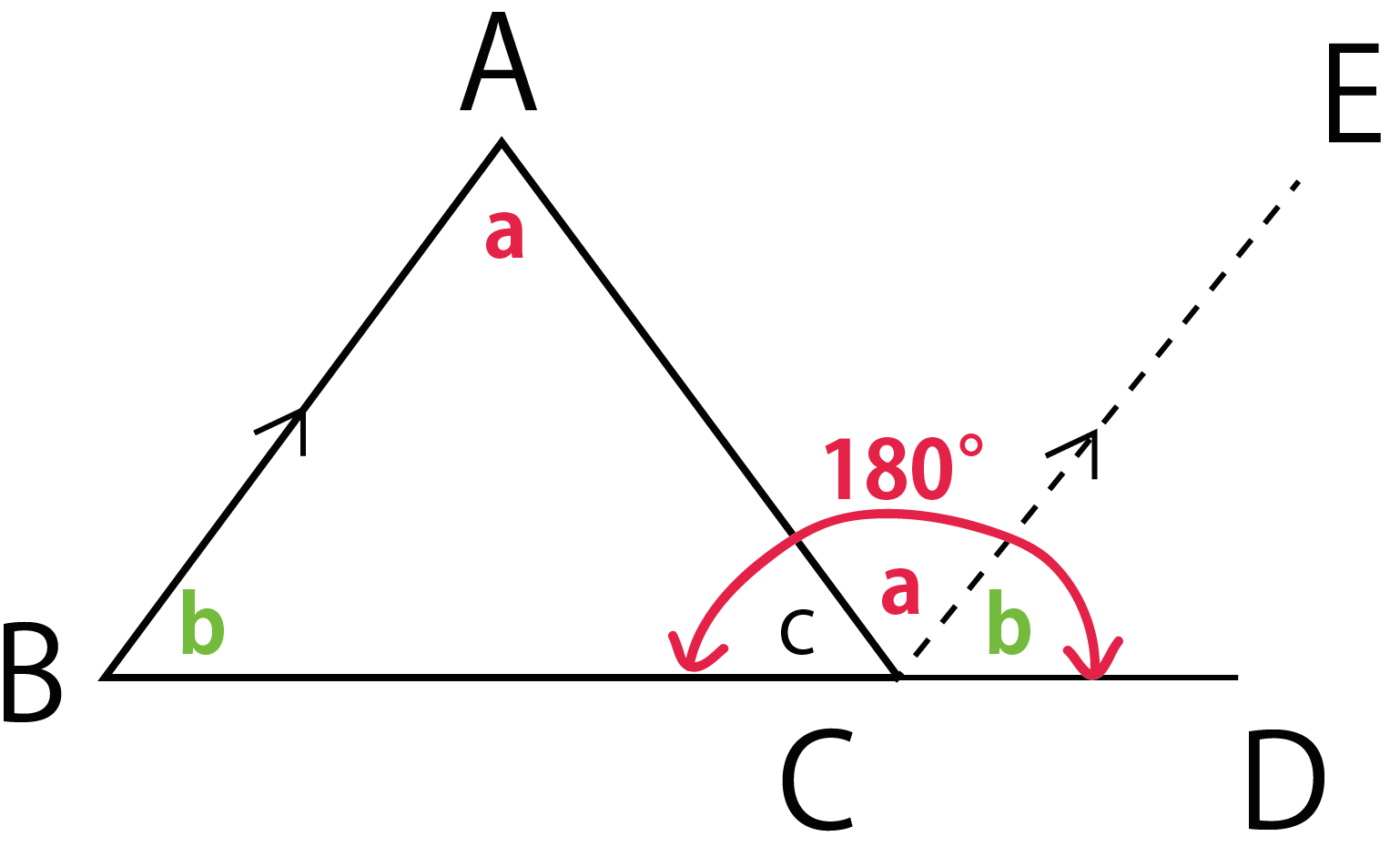



中2数学証明 三角形の内角の和の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



从半年报业绩预告看经济恢复情况 江海债券日报21 07 05 债券 参考财商报
一方、エは8cmの辺の一方の端に30°があり、離れたところに70°の角があります。 三角形の内角の和が180°であることを利用すると、180°-(30°+70°)=80° より、もう一方の端の角が80°であることがわかります。 よって、合同条件「1組の辺とその両端の角がそれぞれ等しい」を満たします。 HI=LK=8cm、∠H=∠L=80°、∠I=∠K=30° なので、 GHI≡ JLK 合同ユークリッド空間 では、三角形の角度の 合計 は等しい 直線角度 (180 度 , π ラジアン 、2つの 直角 、または半回転 )。 三角形 には3つの角度があり、各 頂点 に1つずつ、隣接する 辺のペアで囲まれて



Z0yaie1jbvwlum
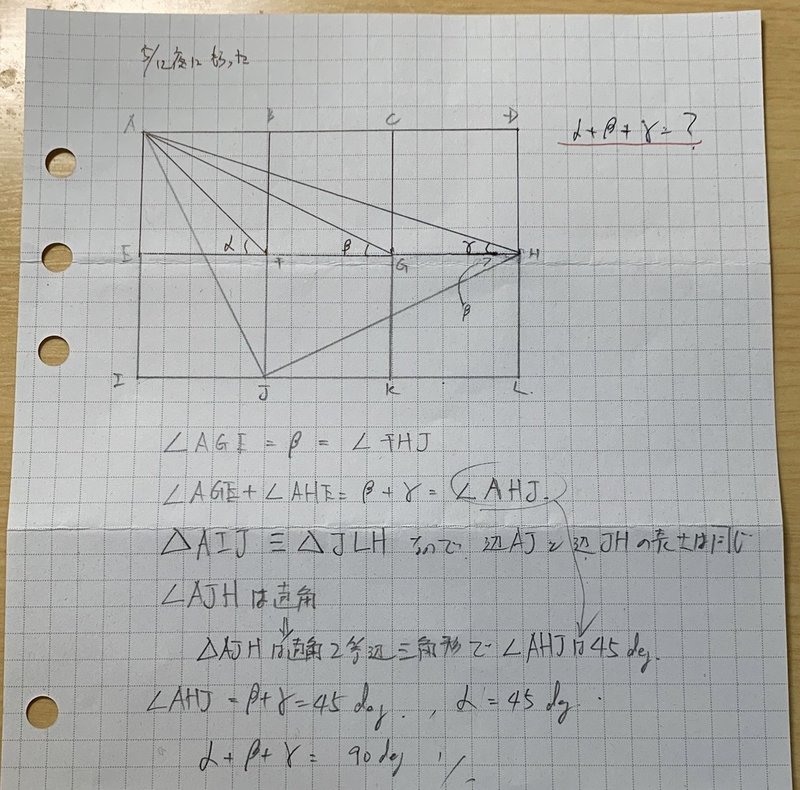



幾何 三角形の角度合計 Nakagaki Note
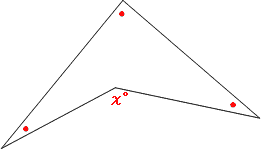



角度の求め方 算数の教え上手 学びの場 Com



1



縫紉王 多角度透明拼布尺60度三角拼布尺六角形拼布尺45度菱形拼布尺60度菱形拼布尺鑽石梯形壓克力尺
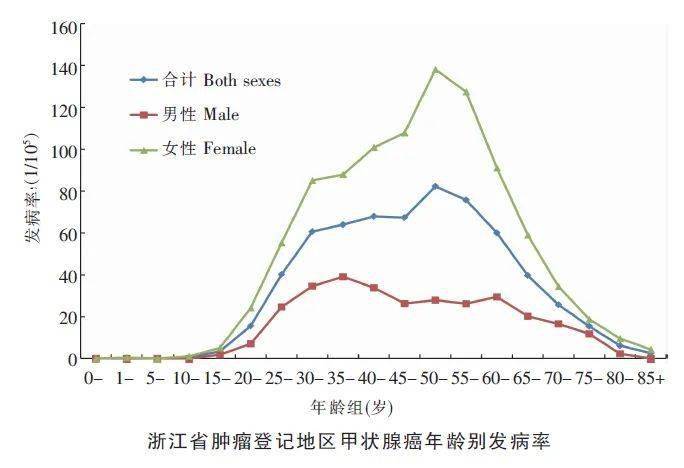



可惜 0岁死于肾癌岁死于胃癌25岁死于肠癌30岁死于肝癌 9位顶尖专家解读浙江最新癌谱 肿瘤
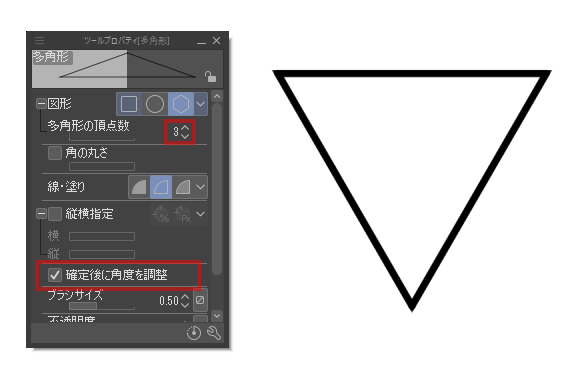



如何繪製倒三角形 擺姿勢 Clip Studio Ask




A股三大指数震荡整理氢能源概念股掀起涨停潮 A股 热门股 A股市场 各板块 网易订阅
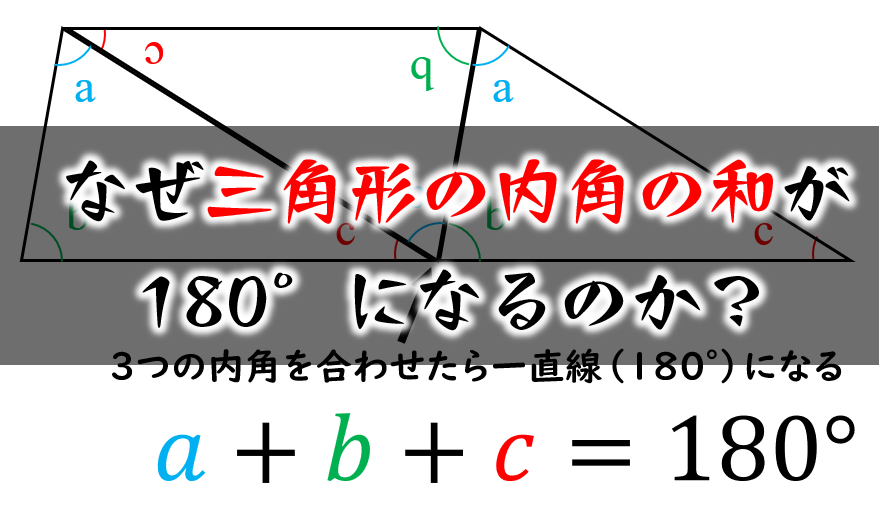



三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun
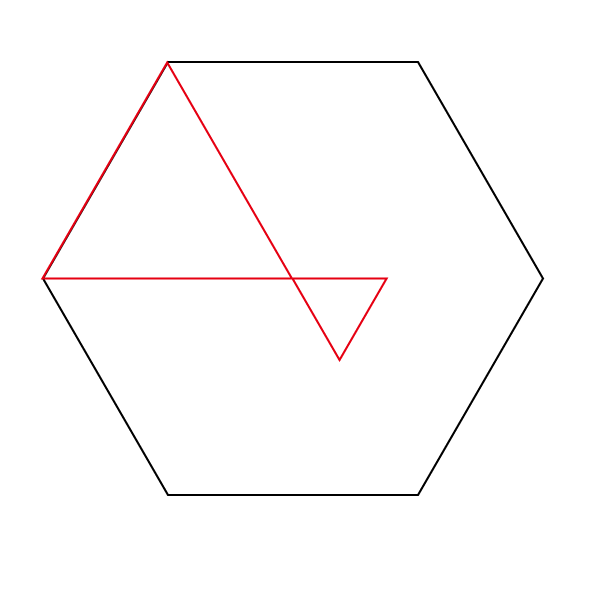



角度情報がない図形の合計の角度 星形多角形 受験算数入門



Http Science Hsjh Chc Edu Tw Upload Works 106 603bf5ac4dee6efa22ee38d5c0f0cbb5 Pdf



用球面三角函数计算可转位刀具的空间角度 信息图文欣赏 信息村 K0w0m Com




亚洲市场自保态度 Willis Towers Watson



Http Pdf Dfcfw Com Pdf H3 Ap 1 Pdf



直角測量量角多功能加厚不銹鋼直角尺90度角尺角度尺拐尺木工尺三角尺組合角尺量角 蝦皮購物




高科大 捐贈興學網



风电装机目标大超预期 这家公司订单饱满 业绩即将释放 财富号 东方财富网
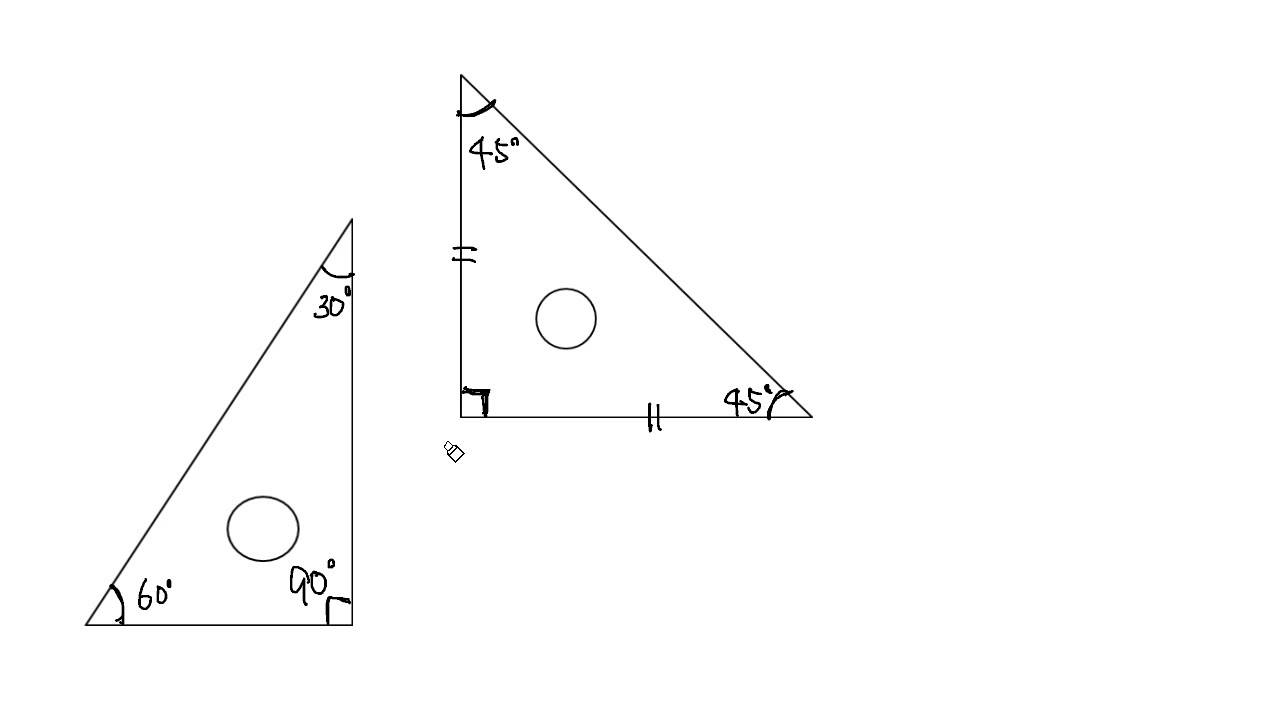



三角形の内角の和 Youtube



厉害 这个大咖押中高考130分
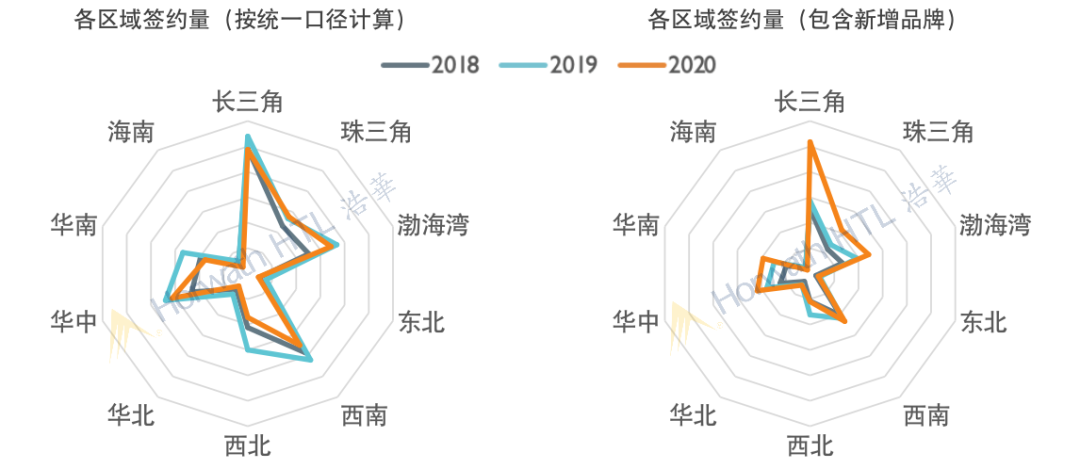



去年酒店新增签约数量直线下滑 中端品牌签约数同比降40 环球旅讯 Traveldaily




誰說三角形的三個角加起來永遠是180度 一流人 遠見雜誌




初中數學培優八年級下第19講圖形的摺疊 分割和拼接中考必考 每日頭條




樂思精英班數學科重點訓練小二下數學練習 教科書 Carousell



昌爸挑戰題
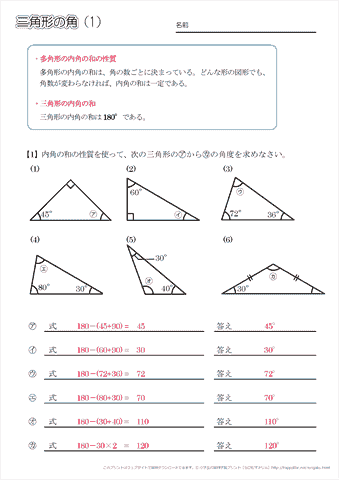



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学



Http Wvb Com Corporations Update Download Src Mnt Pdf Mount Reports Chn 000 040 Chn A 01 L 12 31 Pdf




失踪的正方形 维基百科 自由的百科全书
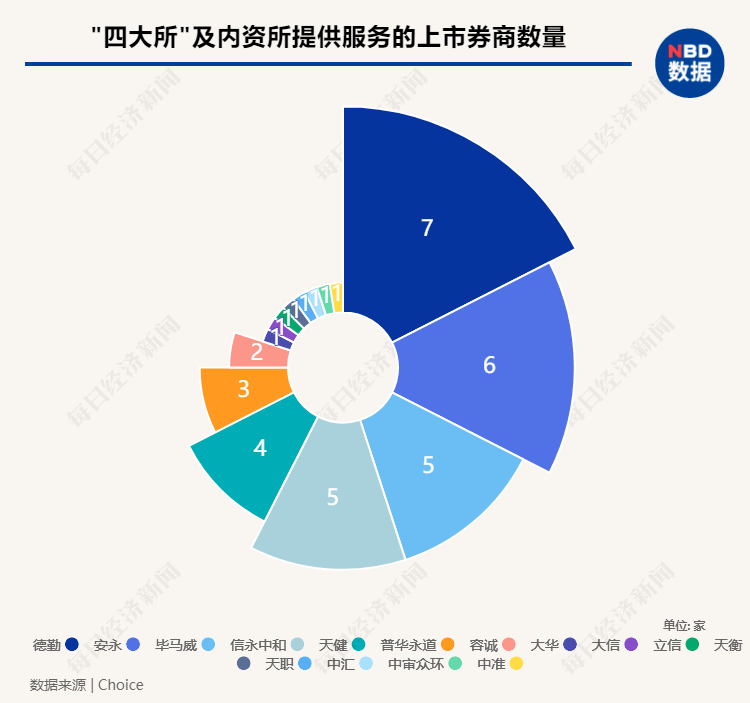



一纸靠谱的审计报告究竟有多值钱 有券商豪掷600万 有券商节约150万全靠这一招 费用



Www Boyo Org Tw Boyo Index Php Downloads Category 54 17 12 11 01 34 41 Download 1764 Pdf Start




角度を計算する方法 9 ステップ 画像あり Wikihow
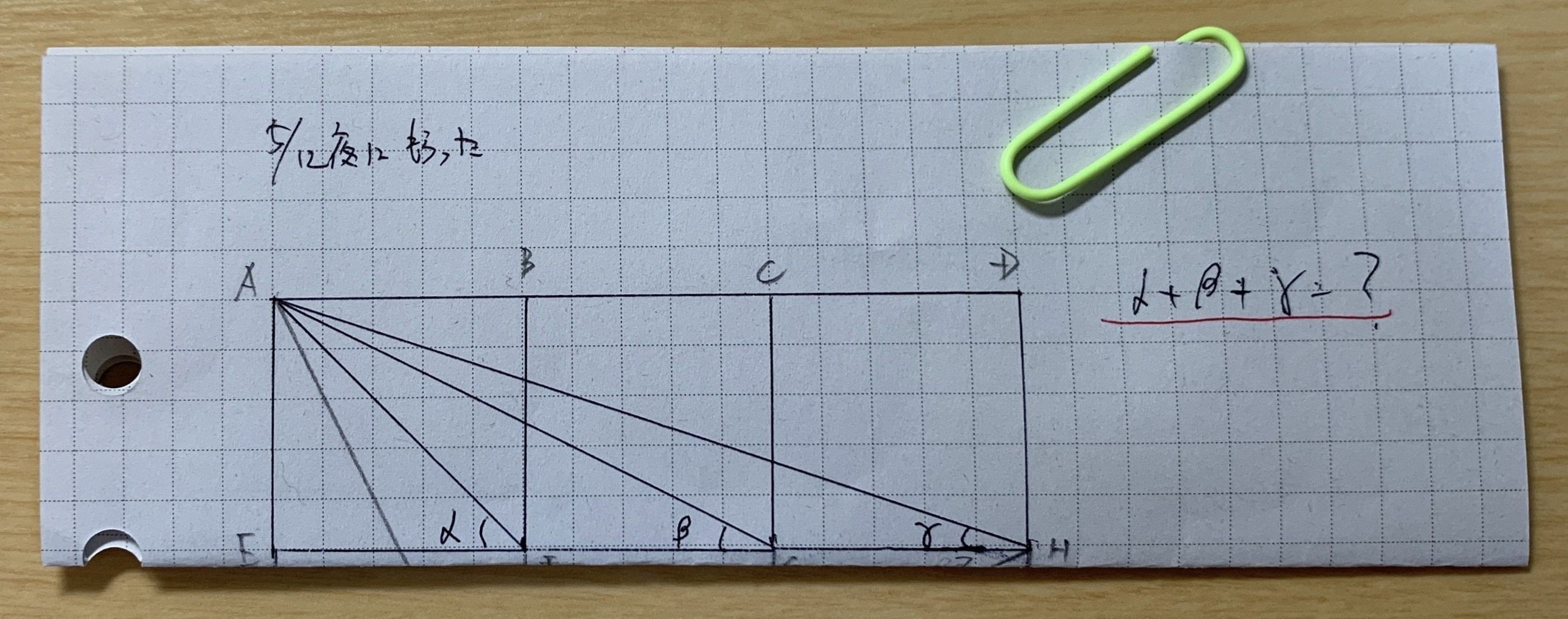



幾何 三角形の角度合計 Nakagaki Note



誰說三角形的三個角加起來永遠是180度 一流人 遠見雜誌




0到360度三角函數值表 特殊角的三角函數值表 每日頭條
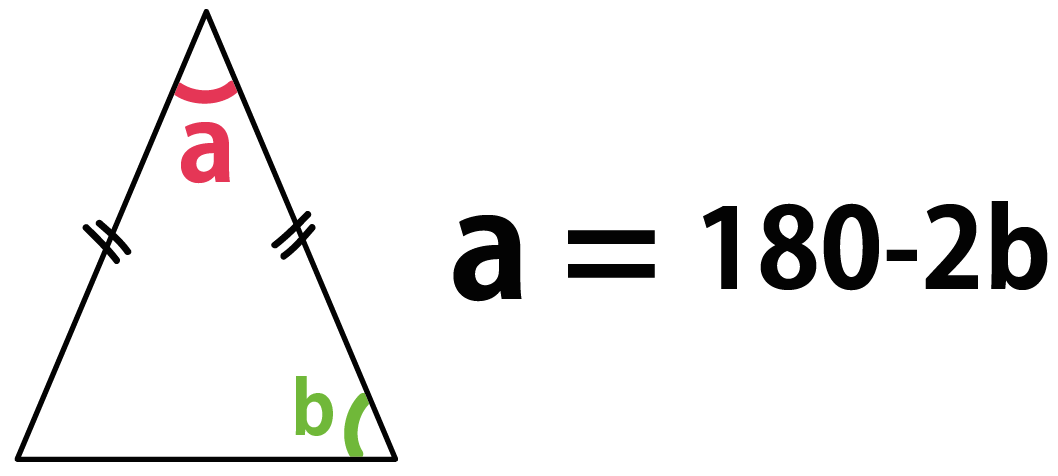



簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく



Core Ac Uk Download Pdf Pdf
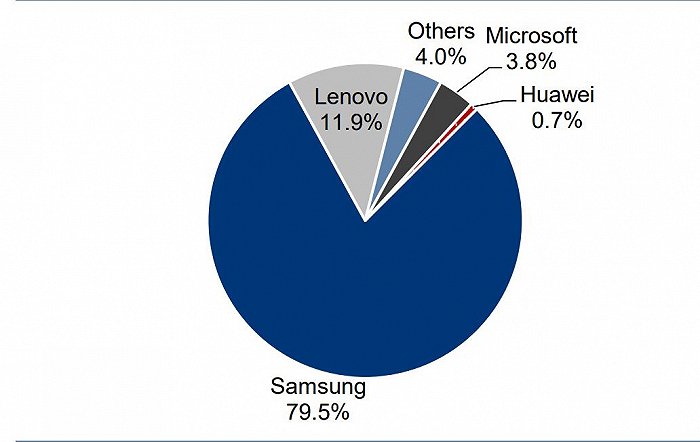



Matex2预约300万部 折叠屏手机真火还是虚高 界面新闻 Jmedia
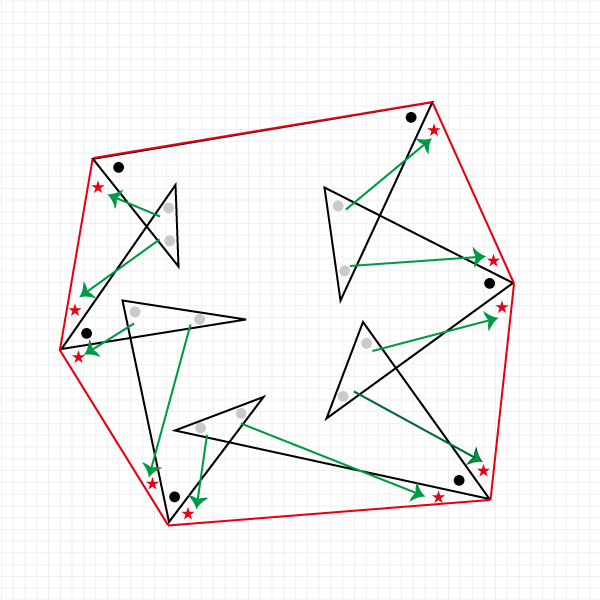



角度情報がない図形の合計の角度 星形多角形 受験算数入門
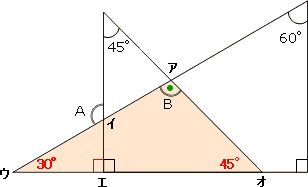



角度の求め方 算数の教え上手 学びの場 Com



Http Rportal Lib Ntnu Edu Tw Bitstream 500 1 s01 Pdf



Www Boyo Org Tw Boyo Index Php Downloads Category 54 17 12 11 01 34 41 Download 1764 Pdf Start
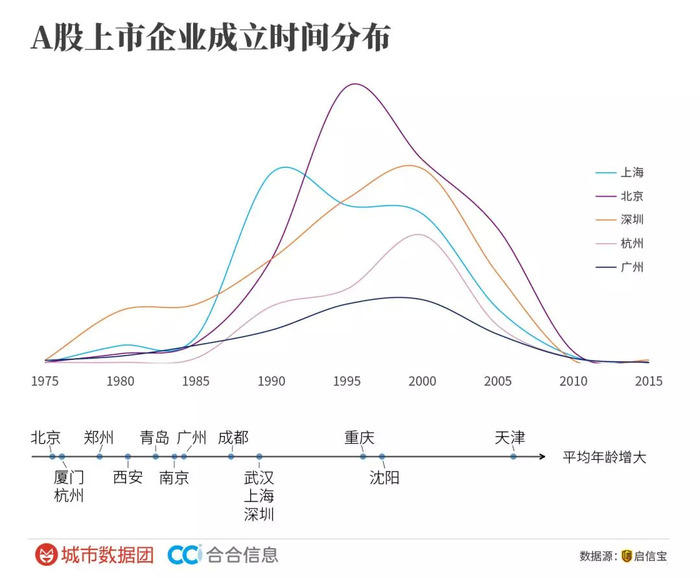



数据 股民朋友 中国城市a股上市企业数量排名了解一下 界面新闻 Jmedia




三角形的類型 急性和鈍性




印刷可能 三角形角度合計 犬イラスト




中学受験のための学び方参考書 ここから算数 しっかり基礎力 Amazon Com Books




印刷可能 三角形角度合計 犬イラスト




角度を計算する方法 9 ステップ 画像あり Wikihow




角度を計算する方法 9 ステップ 画像あり Wikihow



直角三角形角度計算公式 直角三角形角度計算公式線上資訊以及角度計app認知角度計app 共68筆1 1頁 App開箱王




三角形的類型 急性和鈍性



用球面三角函数计算可转位刀具的空间角度 信息图文欣赏 信息村 K0w0m Com



Zf Ebyjgyw7h M



三角尺 插圖素材 圖庫



三角尺插圖素材尺子文具測量尺子書寫工具矢量 插圖素材 圖庫



紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 13



Http Web Math Sinica Edu Tw Math Media D391 Pdf



用球面三角函数计算可转位刀具的空间角度 信息图文欣赏 信息村 K0w0m Com




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学



Material Hle Com Tw Wp Content Uploads 21 03 E5 9c 8b E4 B8 Ad E6 95 B8 E5 Ad B8 E5 Bf Ab E6 95 B8 E7 92 E6 87 80 E5 A5 E7 B4 A0 E9 8a Pdf



Http Science Hsjh Chc Edu Tw Upload Works 106 603bf5ac4dee6efa22ee38d5c0f0cbb5 Pdf



Http Rportal Lib Ntnu Edu Tw Bitstream 500 1 s01 Pdf



直角三角形角度計算公式 直角三角形角度計算公式線上資訊以及角度計app認知角度計app 共68筆1 1頁 App開箱王



6df3 Zsxgmwkum
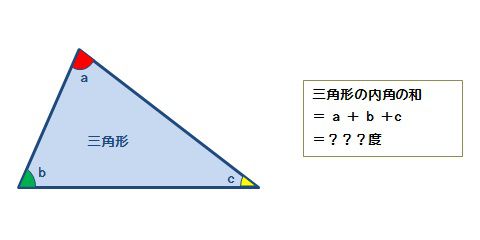



三角形の内角の和 算数の公式覚えてますか



好风凭借力 扬帆正当时 长城创业板指数增强基金投资价值分析 基金研究投资网
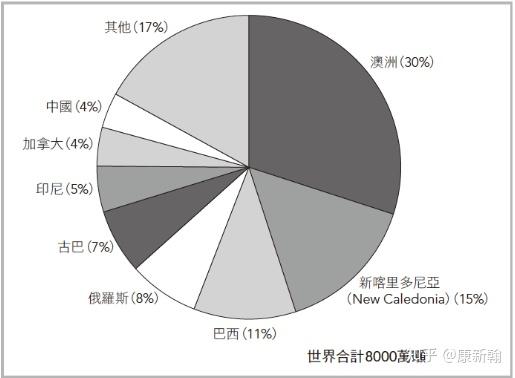



金属镍 原物料角度分析 知乎



用球面三角函数计算可转位刀具的空间角度 信息图文欣赏 信息村 K0w0m Com




三角形的類型 急性和鈍性
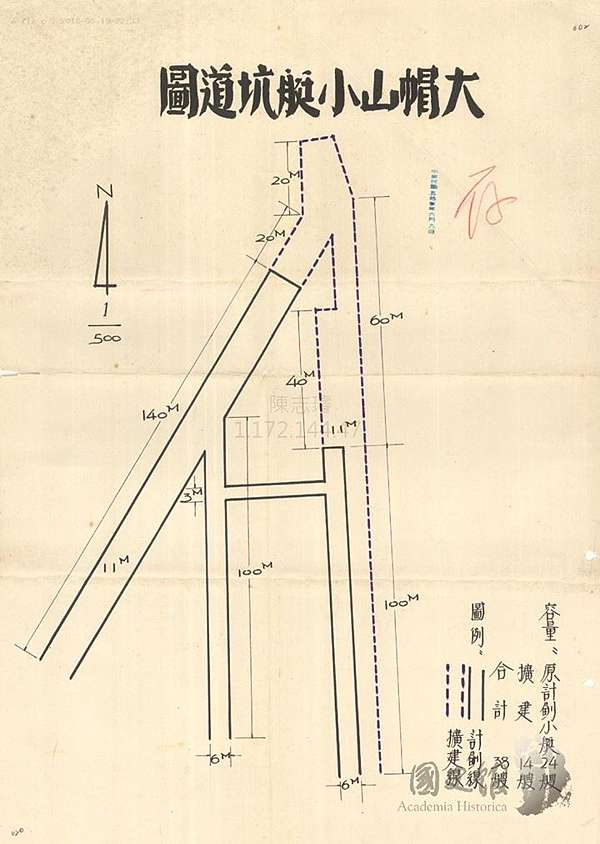



翟山坑道 一個無法挽回的歷史錯誤 金門戰地史蹟論壇 記錄金門戰地戰史 見證金門戰地歷史 痞客邦



直角三角形角度計算公式 直角三角形角度計算公式線上資訊以及角度計app認知角度計app 共68筆1 1頁 App開箱王



第二章一般設計通則




三角形の角度から分かる 宇宙の形 とは Gigazine



T3yopnrttuui M



Www Cpshs Hcc Edu Tw Resource Openfid Php Id 4348 Fd 1




印刷可能 三角形角度合計 犬イラスト




19數感盃 21數感盃青少年數學寫作競賽




Excel職場新人300招 函數 圖表 報表 數據整理有訣竅 原來這樣做會更快 三民網路書店



縫紉王 多功能多角度圓度切割繪圖壓克力尺xcm 拼布尺 生深淺布可用 縫紉尺diy 縫紉工具扇形尺 蝦皮購物



Http Ntcuir Ntcu Edu Tw Bitstream 4511 2 96 Pdf




前海开源王宏远 全球经济基本面很差 不支持目前估值水平 短线尽量不要加杠杆 证券时报网




和用英语怎么说 百度问答 沪江英语




三角形の内角の和が180 なのはなぜ 小学生に教えるための解説 数学fun
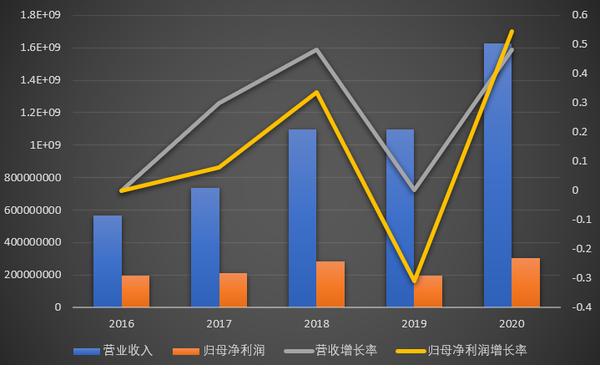



旭升股份 年财务报表分析 知乎




好方啊 我的數學是 不 我可能根本沒上過學 每日頭條
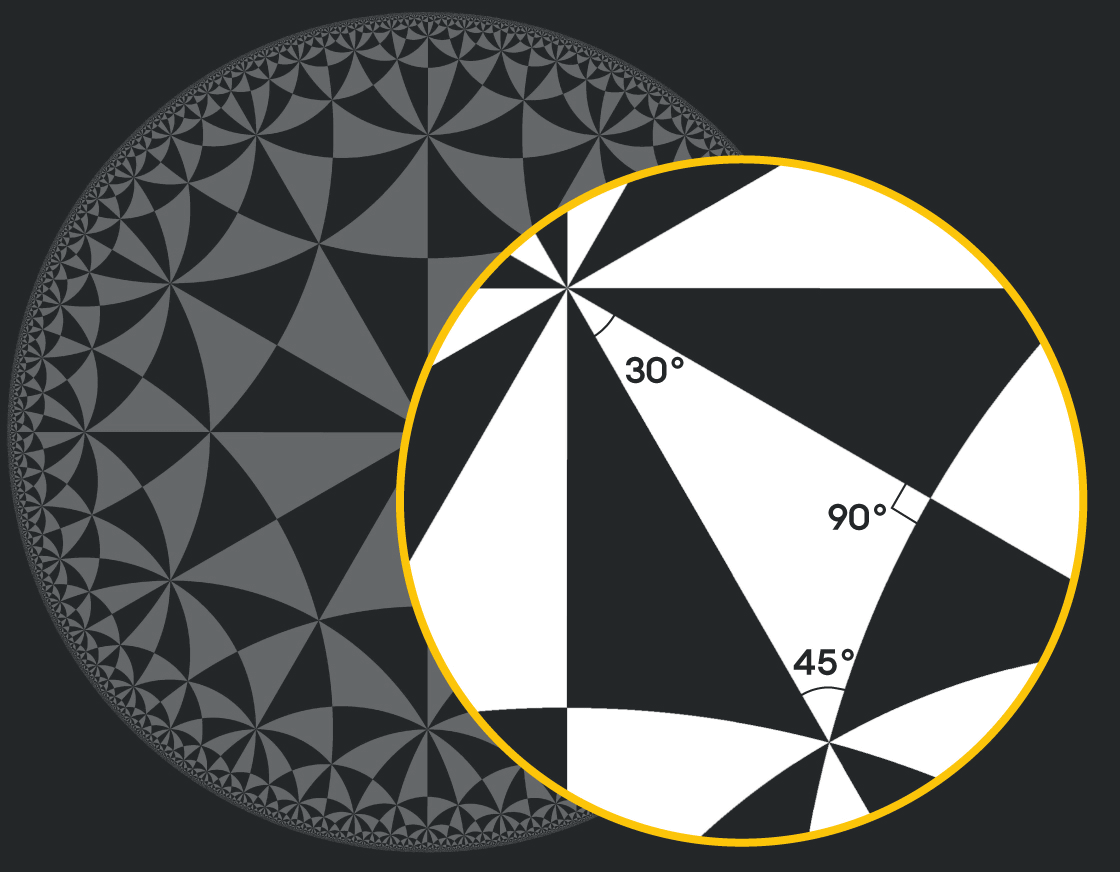



三角形の角度から分かる 宇宙の形 とは Gigazine



Ocr实践系列 East理解及实现



新点软件ipo 现金流承压仍合计现金分红5 2亿存疑 腾讯新闻


