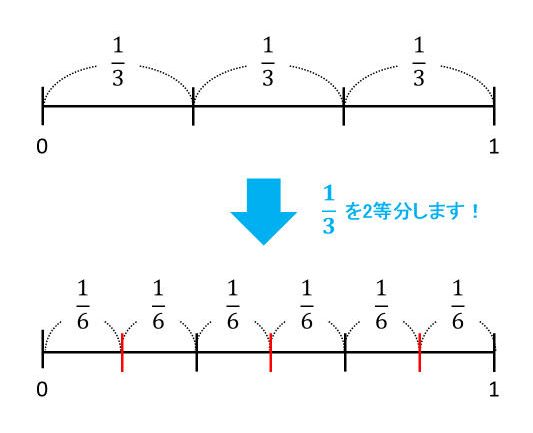
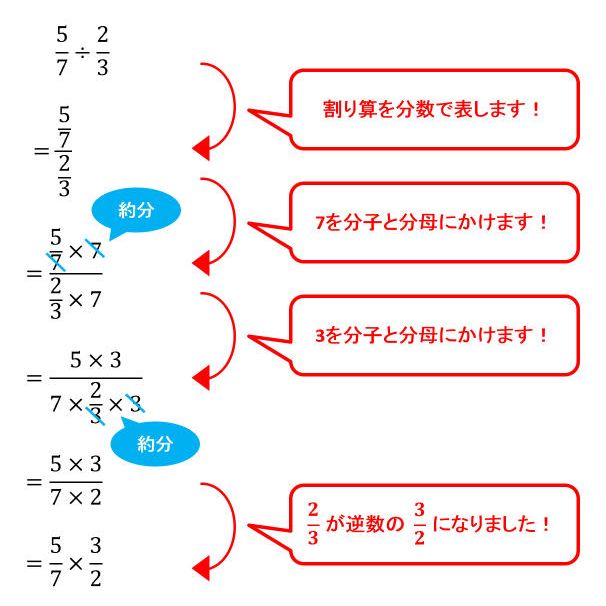
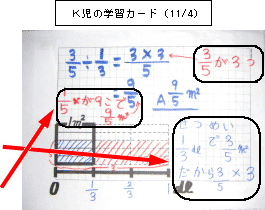
1÷ \large\sf {\frac {2} {3}} のように、割る分数の分子が1でないときを考えてみましょう。 わる分数を分子と分母に分けます。 \large\sf {\frac {2} {3}} = \large\sf {\frac {1} {3}} × 2 (魔法のルール①: \large\sf {\frac {2} {3}} は1つのものを3等分したものが2個) ですので、1÷ \large\sf {\frac {2} {3}} は、1を \large\sf {\frac {1} {3}} で割ってから 2 で割るという2ステップに分けられ単元4 の前半 分数×分数 分数をかける計算 ① (教科書P43~44) ※ スマートレクチャー「P43 1」を視聴しましょう。 https//wwwyoutubecom/watch?v=YAINeHwmMq0&feature=youtube ※ P43 にあるQR コードを読み取り、数直線や関係図のかき方を確認する。 問題 4 5 × 1 3次時の ÷ の追究では,N児は面積図で答えを求めることができた。一方,面積図に抵抗を感じたK児は,N児のつぶやきを意識しながら,いったん計算のきまりで解いてから面積図に戻って追究をする姿が見られた。 5.おわりに
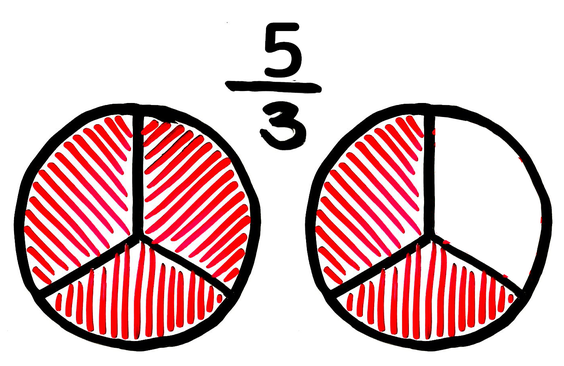
分数の理解が難しい児童へ 量イメージ から 帯分数 を色で描こう 図式
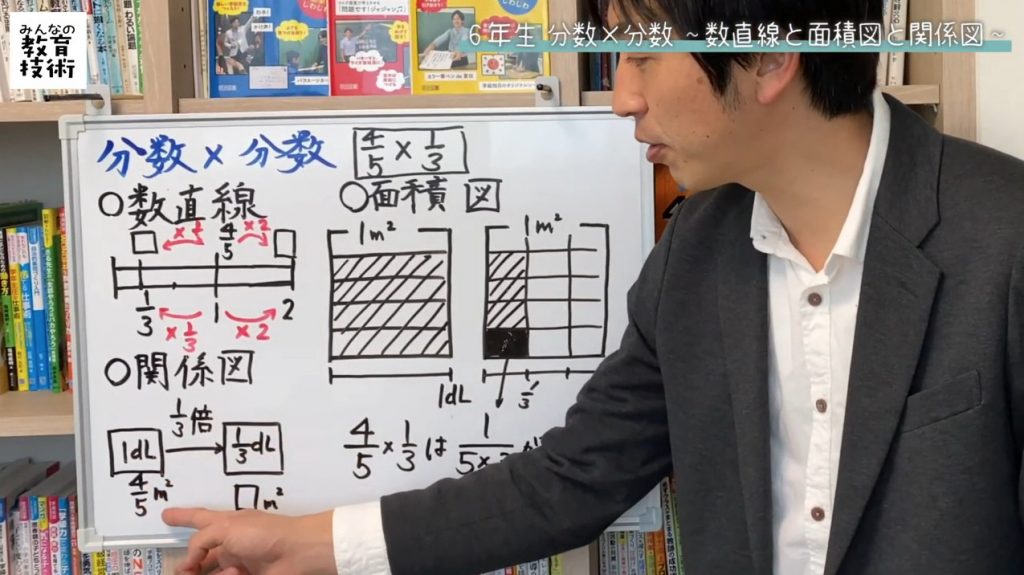
分数×分数 図
分数×分数 図-めあて4/5 × めあて4/5×1/3 めあて4/5×2/3 めあて分数×分数 3の答えを面積図 の答えを面積図で調 の答えを面積図で調 の計算のきまりを見つ を使って調べよう。 べ、説明しよう。 べ、説明しよう。 け、確かめよう。② 分数×分数の考え方を理解することができない。 ③ 既習事項の理解が曖昧なため計算を間違える。 ④ 約分をし忘れて間違える。 ⑤ 小数の逆数で間違える。 ⑥ 倍の問題でわり算が出てくることで混乱する。 ⑦ 割合の問題で、数直線面積図が書けない。



これで分母は足さないぞ 分数の足し算はこういうことだ 福岡 筑豊の家庭教師
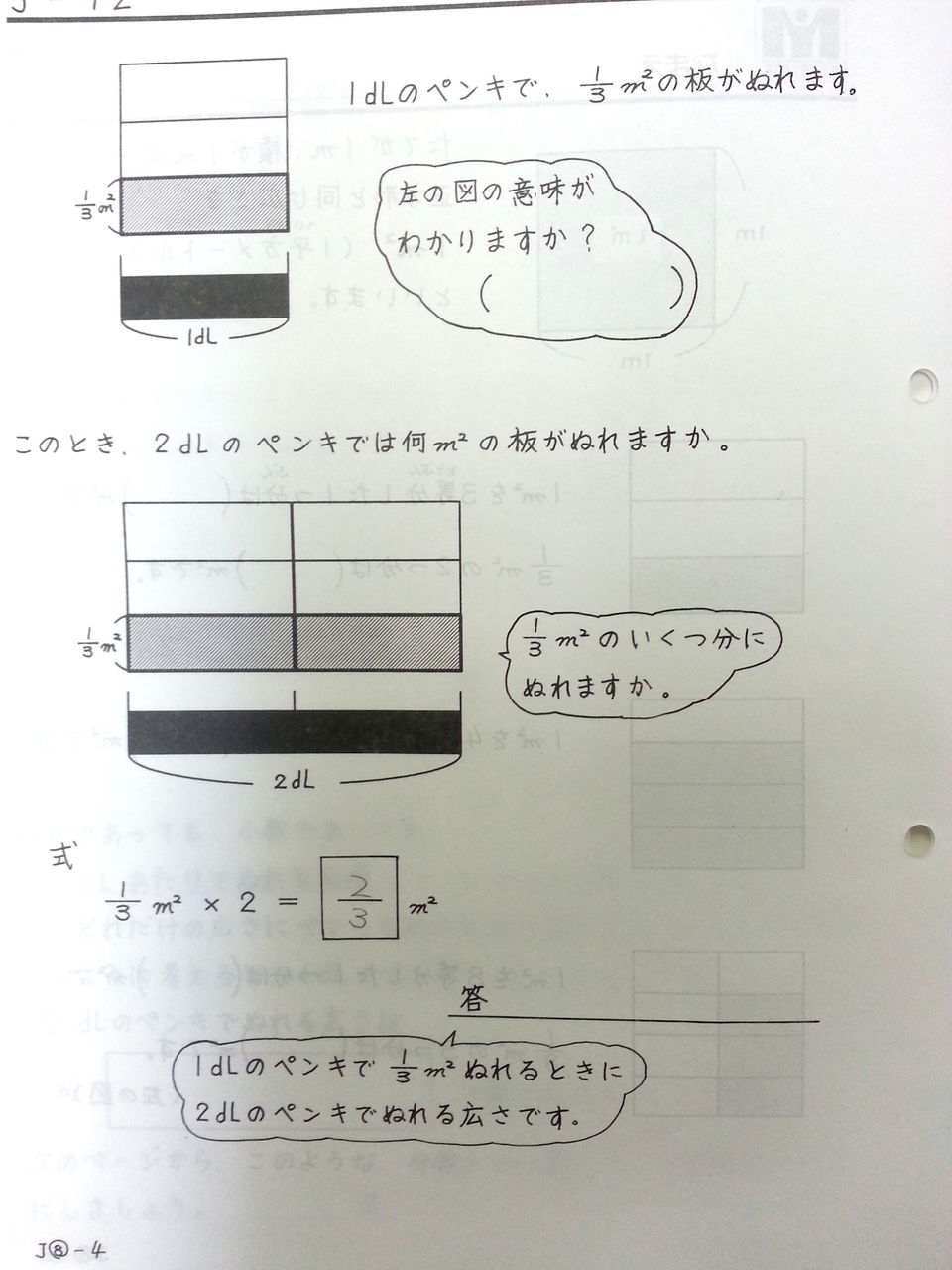
整数×分数 「×分数」の第2時は,かける数が単位分数から,分子が2以上になる一般分数になります。 ただし,かけられる数の方は量感をつかみながらやれるよう「整数」で取り組んでいきます。 問題文を「音読」し,それを聞いて「四ます関係面積図(分数)×(分数)の計算の仕方を,既習の分数の意味や計算の仕方を基に考えることができる。 4 本時の評価規準 数学的な考え方 言葉や数,式,図,数直線を用いて, をかける乗法の計算の仕方を基に, をかける計算の仕方 1|3 2|3上の図のように赤い部分が何個あるかを 考えると計算のしくみがわかってきます。 説明ができたら、計算のしかたをノートにまとめましょう。 このことから、分数×分数の計算は次のようになることを教えます。 とても重要です。覚えましょう。 教え方2
「分数×分数」の計算に意味を理解するための教材です。 分母、分子の変更ができます。数字をクリックして、訂正し、 をクリックするとその数値にあわせて図が変更されます。オレン ジ色の四角形を移動して、その合計がいくつになるかを確かめ、(分数)×(分数)の計算のしか たを,既習事項をもとに,数直線 や図,表,式を用いて考える力を 養う。 、乗数や除数が整数の場合の分 数の乗法及び除法の計算のしかた を考え,それを活用しようとする 態度を養う。 、(分数)×(分数)の計算のしか分数×整数の方法がわからなくても、答えを出すこ とはできる。 A ゴリ蔵さんの考え(図で考える) 1g でぬれる面積は 3 7 ㎡だから、右のような図をかくことができる。 これが「×2」で2こ分あるということだから、 7 となり、これらを1つにまとめると、
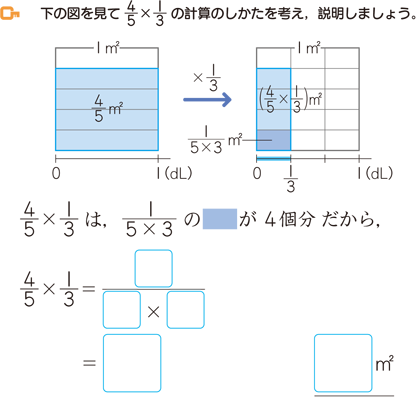
(分数)×(整数)の計算の仕方を考えることができる。 <問題①> 3 5 考え方1 図(面積図)を使って考える方法(スマートレクチャーを見ながらやってみよう) 1 5 (1)左の図の 3 5 に赤で色をぬろう。 (2)右の図の( 3 5分数×分数 分数÷分数 の授業について (授業を始める前の状況) ・計算方法を知っている子どもは多い。 ・計算ができれば、それでよしとする考え方もある。そうすれば、ここの単元は、半分以下の時間数 で終了することができる。「分数×分数」 教科書42ページ~43ページ 月 日( ) 名前 1 教科書42ページの問題を声に出して読みましょう。 (1) ペンキの量が2dLや3dLのときに、式はどうなるのかを、教科書の ような図で考えまし
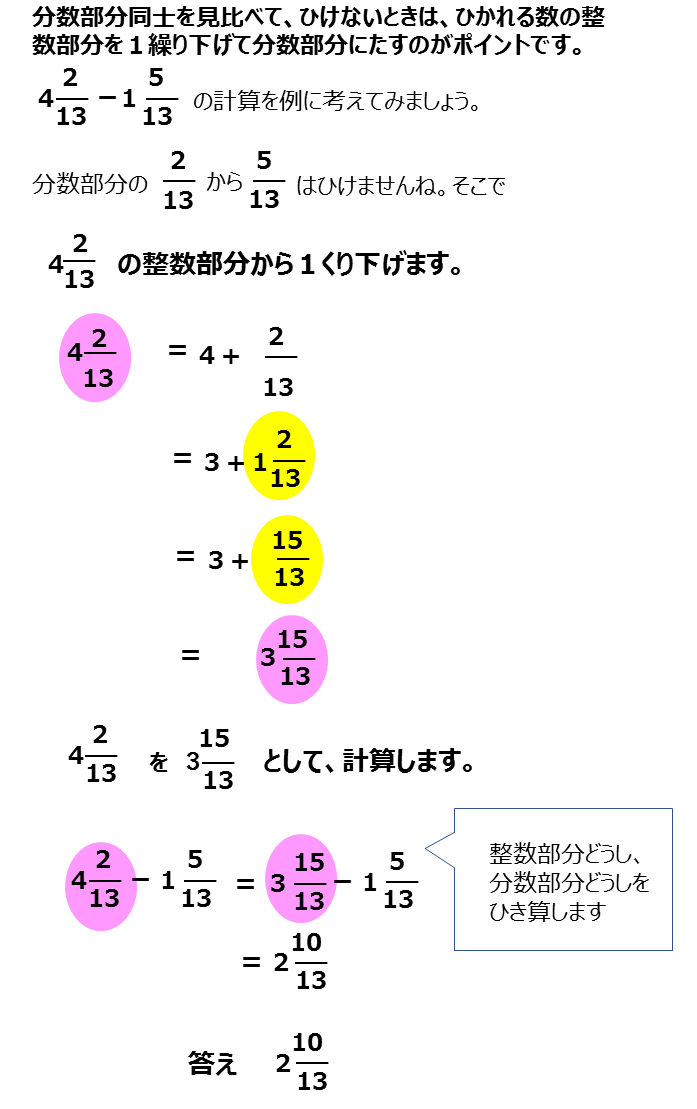



分数 帯分数のひき算 算数 教科質問ひろば 進研ゼミ小学講座




B 2 1i See How To Solve It At Qanda
図形 「円」の面積 「おうぎ形」の周と面積 「立方体・直方体」の体積 「角柱・円柱画像一覧 「分数×分数」導入 「分数×分数」の単元に入ります。 導入は「整数×単位分数」です。 教科書ではいきなり分数と分数をかけていますが,その場面では具体的な「量」を意識しながら考えられる児童は少ないでしょう。 まずやるべきことは「分数をかけるとはどういうことか」をイメージすることであり,まず単位分数をかけることの意味をしっかり算数レポート練習「分数のかけ算の仕方」 p45「 5」①~④を練習ノート(黄色)にする 5 分数×分数の計算の仕方 ~整数や帯分数,小数をふくむ場合~ 教科書p46,47 計ド19 計ド 計ド21①~⑨ ?分数のかけ算に整数や帯分数,小数が入ってきたらどうするの?




なぜ分数の割り算はひっくり返すのか お試し版
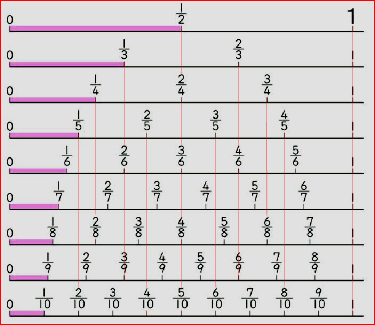



4年算数 分数 2 わかる教え方のポンイト
③分数 ×分数 では ,言葉 の式や数直線 ,面積図 を用いながら ,「1つ分×いくつ 分=全体 量」のかけ 算の関係 を捉えさせる 。単位分数 の何倍 になっているのか ,かける 数を整数 にし分数×分数の計算に習熟する。 ㋐㋑ B 割合を表す分数のかけ算の問題を解決する。 ④㋐ 関係図や線分図を使って、数量の 数量の関係をとらえることができるように、何 5 C 割合としての分数 関係をとらえる。 を1と見たときの割合なのかに着目させる。③図 3 5 ① ②式 ④ 3 5 分数のかけ算・わり算① ① 分数×整数 復習問題 1まい2㎡の絵を4まいならべると、何㎡になりますか。 ④ 答え 問題1 1まい 1あたり量 ㎡ いくつ分 全部 1まい まい ㎡ ⑤ 答え ㎡の板を4まいならべると、 何㎡になりますか。




分数のわり算 等分除 包含除 を数直線で かけ算の順序の昔話
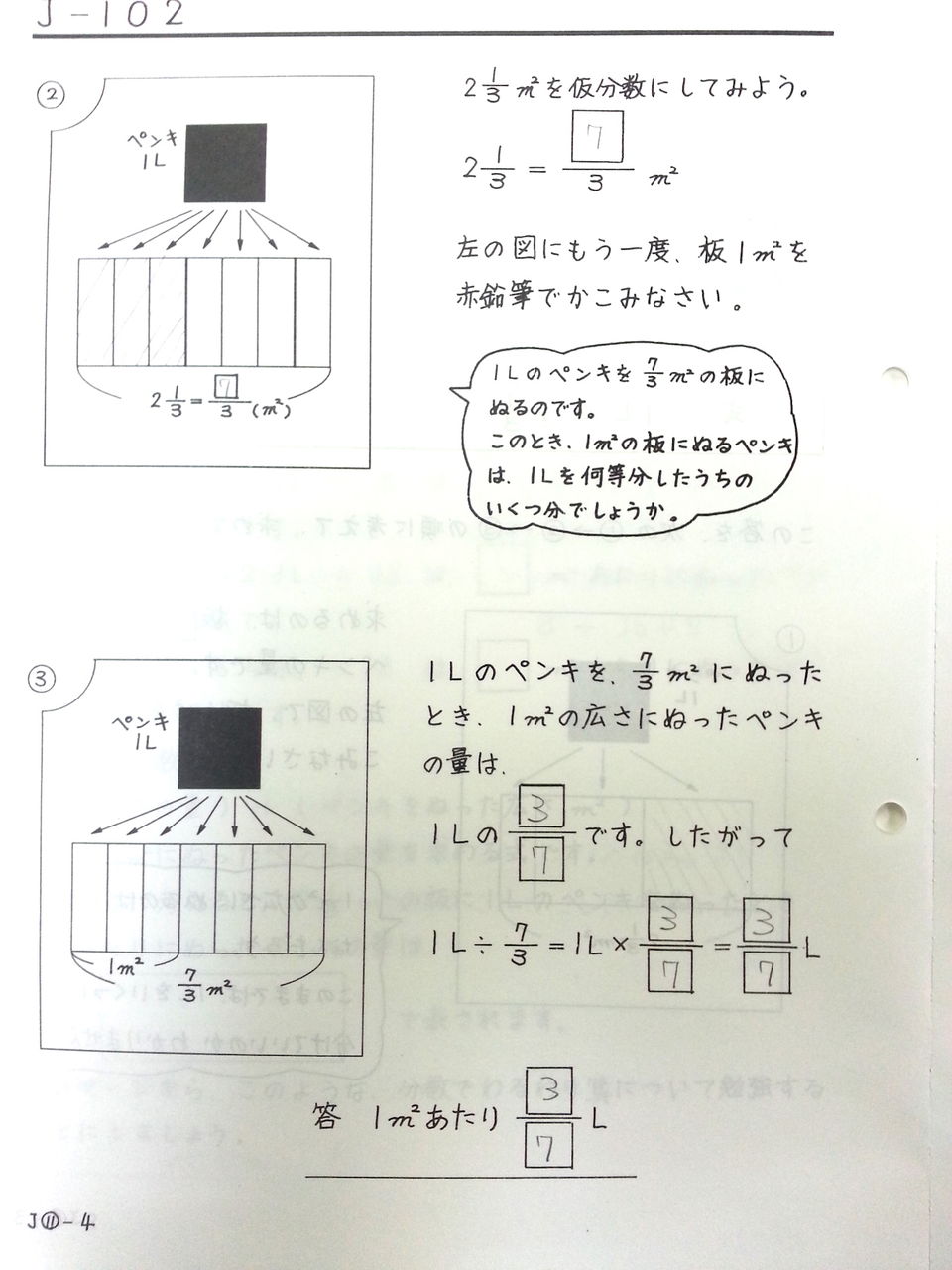



分数が苦手 を克服するために 4 小 中学生向け補習塾 算数 数学 国語 ほめるん By じりつ堂
分数の掛け算はなぜ分母同士・分子同士をかけると計算できるのでしょうか? 小学6年生向けに分かりやすい方法を教えていきます。 目次 非表示 1 どんな計算も整数に直すことが基本 2 分数×整数分数÷整数の形にすれば計算できる! 3 整数に(分数)÷(分数)の計算の仕方を図や既習事項を基にして考え、説明する 子どもから出された考え わり算のきまりを使って 3 2 ― ÷ ― 5 3 3 2 5 3 ②わり算のきまりを使って 3 2 ― ÷ ― 5 3 3 3 2 3 =( ―×―) ÷( ―×―) 5 2 3 2 ― 5 5小学6年生の算数 分数のかけ算|分数×整数・分数×分数 練習問題プリント 小学5年生で習う「分数×整数」のかけ算と、6年生で習う「分数×分数」のかけ算のルールを確認して練習できる問題プリント。無料ダウンロード・印刷できます。



通分の変化が見える 分数たし算 のイメージ式を色で描こう 図式



Q Tbn And9gcss0o 8ql7pehutb Oxyth9kdazsykhhtkkud7knvmwbdss5nvg Usqp Cau
今まで「分数÷分数」は①線分図②面積図(区切りが入った図)③たすきがけが主な指導法である。 これらに加えて、面積図(一あたり量×いくつ分=全体の量)を用いた指導を提案したい。 分数÷分数で子どもたちがつまづく可能性のあるのは、以下の3点だと考える。 ①文章題からの立式②逆数のかけ算③約分である。 このうち、②と③は「分数×分数ゲームを通して分数×分数の答えを面積図で視覚的にとらえる。 もとになる大きさや単位分数に目を付けさせ、そこから分数のかけ算の計算の仕組みに気づく。 方 法 <大きく変身! 右の図のようなカードを多数準備する。 (カードは1/2、2/3、3/4、4/5、5/6を数枚ずつ準備) 中から1枚を引きサイコロをふって、目の数だけ倍にする。 カードに何倍したか分数に このペンキ1dLでは、何m²ぬれますか。 どんな式になりますか。 昨日の問題と同じで、1dLを求めている。 式は、 4 9 4 9 ÷ 2 3 2 3 です。 分数×分数の計算は、分子と分母をそれぞれかけて求めることができたので、同じように考えてみよう。 4÷2 9÷3 4 ÷ 2 9 ÷ 3 = 2 3 2 3 分数÷分数も同じように、分子同士と分母同士をそれぞれをわれば、できるね。 この方法は
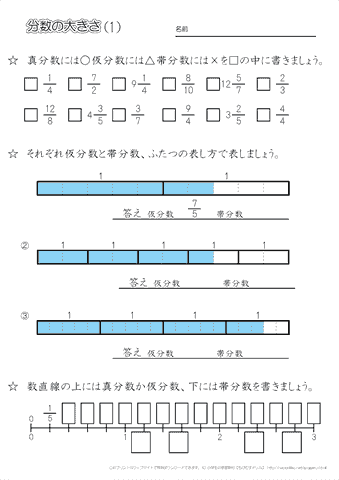



小学生の算数 分数 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 小学生




小学3年生 算数ドリル 分数1 プラス パル
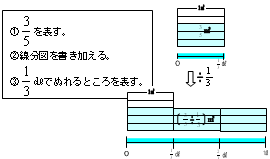
面積図は,数量の乗除の関係を長方形や正方形の形で表 現した図です。 面積図については,5年では,分数×整数や分数÷整数, 6年では,分数×分数や分数÷分数に関して理解を補助 するために使用しています。図を使うと,計算の意味をと3 分数×分数の計算のやり方をまとめる。 紙が ㎡でなくて4㎡だとしたら,何算を 使うかな。 分数×整数の計算のやり方を考えましょう。 ①面積図に色をぬって答えを求めよう。 ④数直線をかいて求めよう。 ①1枚の紙に5分の4塗る。もう1枚に5分の4塗る。図より、( = )という式を見付けることができる。これも、分数のかけ算 と同様、( )の関係から考えて立式したものである。 を求めるためには、 を ( )にしなければいけないので、 を求めるためには、見付けた式を ( = )に変える。




真分数 仮分数 帯分数の自主学習ノート 家庭学習レシピ 学習ノート 学習 小学校 算数



分数のわり算の仕組みを理解しよう 逆数をかけるのはどうして の謎に挑む 中学受験ナビ
第2次 1・分数をかけることの意味を理解考真分数×真分数の計算のしかたを、図 分数のかけ する。 を用いて既習の分数×整数、分数÷整( 算 本・真分数×真分数の計算のしか 数の計算と関連づけて考えている。 4時間時 たを理解する。3 分数×分数の計算のやり方をまとめる。 ③ を整数になおせば計算できる。 かける数を3倍して,積を3でわる。 絵の具が dLでなくて2dLだとしたら,何 算を使うかな。 分数×分数の計算のやり方を考えましょう。 ①面積図に色をぬって答えを求めよう。・分数×整数の式の意味を理解する。 りやすいことを指示して実際にや ・場面見つけをたくさんする。 ってみる。 2/18 分数×分数(単位分数)の計算の仕組み ・ 数直線,テープ図,面積図等を について考える。 もとに,乗数が分数になっても,
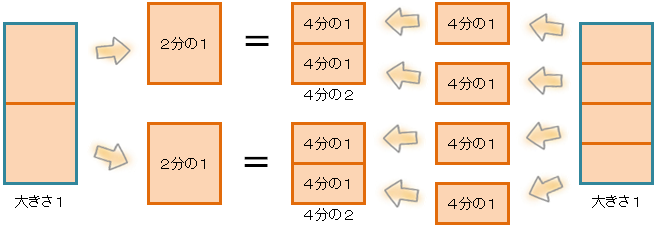



分数の計算 算数をしよう Actaba




小6算数 線分図を2本かく分数の割合 ブログ アビット
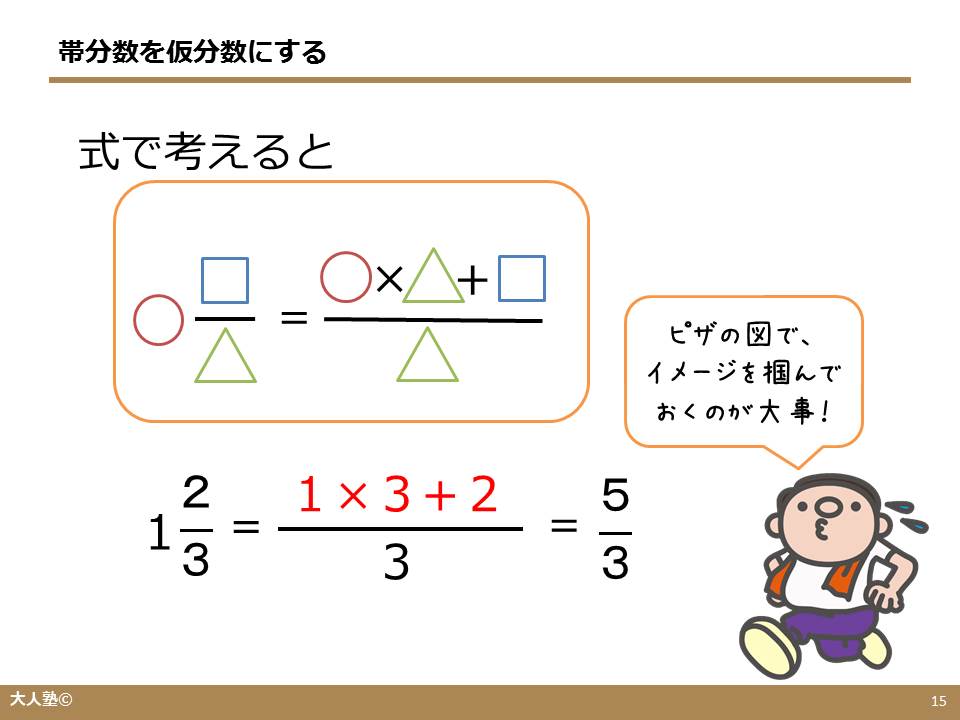



真分数 仮分数 帯分数とは 大人の学び直し算数 計算のやり方解説 無料



分数のかけ算 算数 指導案 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




新版 なぜ分数の割り算はひっくり返すのか 数学ギライも図に描けばすぐ理解できる Amazon Co Uk Books
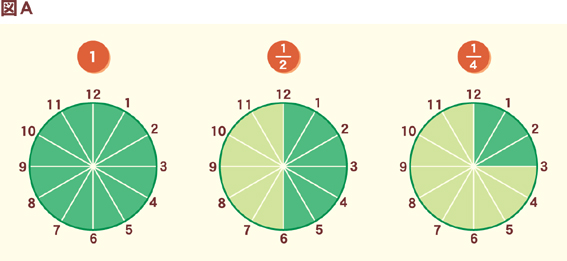



すコラ 08 12 02 わかりやすい分数の割り算は 円図 その1 号外 やまねこ新聞社




分数あてクイズ Geogebra
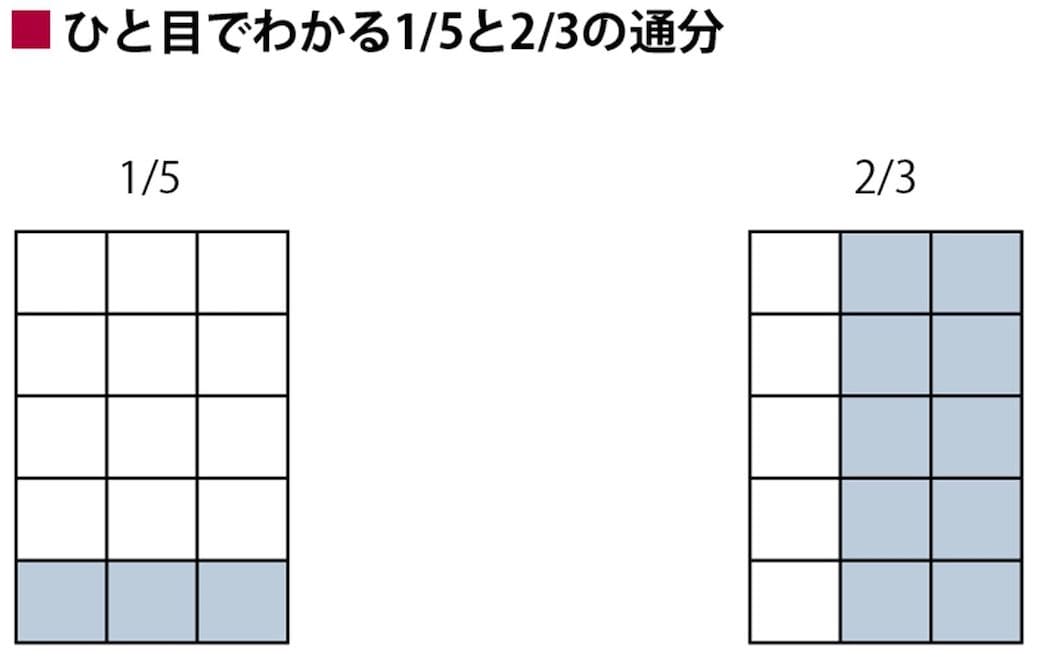



算数も怪しい人が知りたかった分数計算の真髄 子育て 東洋経済オンライン 社会をよくする経済ニュース



学習支援 まなびの函 分数とは 3 真分数 仮分数 帯分数




6年算数 分数のわり算 文章題 面積図を使って解説します 分数 整数 5年生の復習 Youtube
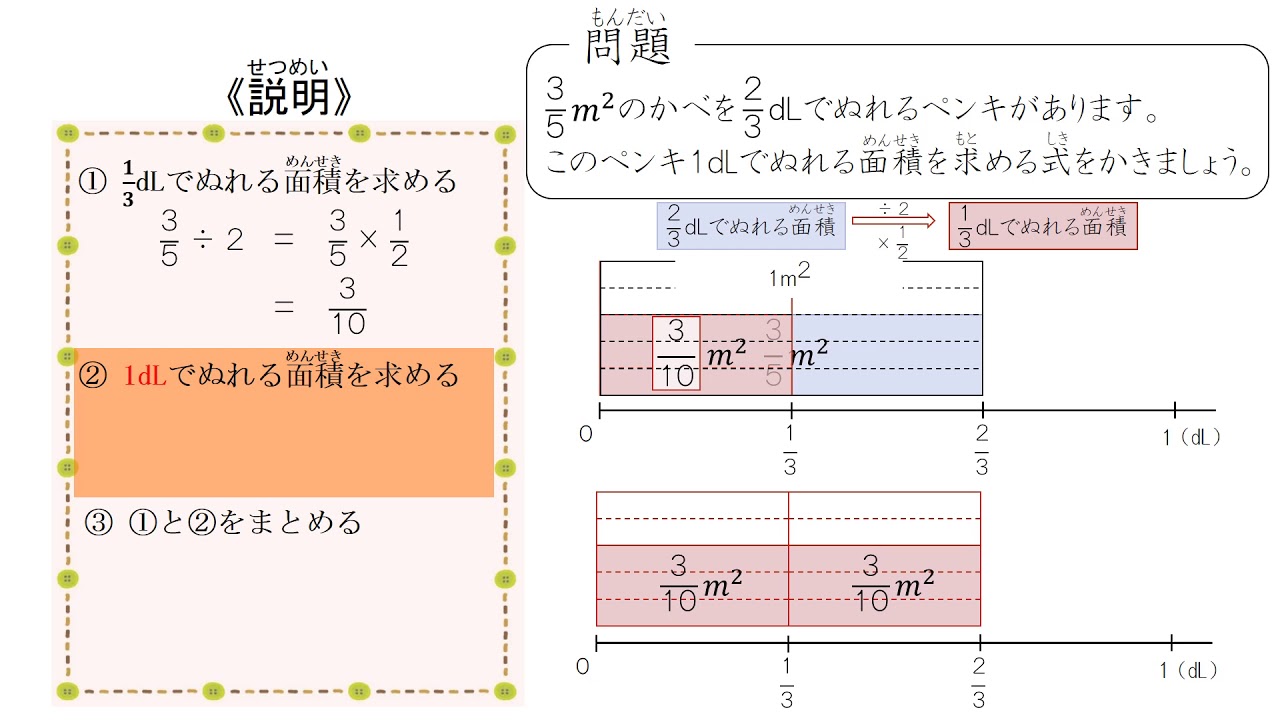



小6 分数のわり算 概念 面積図 日本語版 Youtube
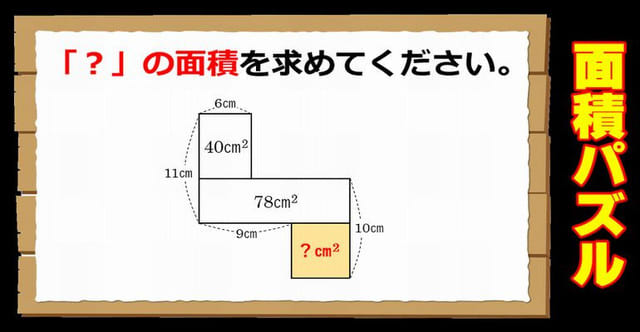



面積パズル 小数や分数を使わず解いてください 暇つぶしに動画で脳トレ
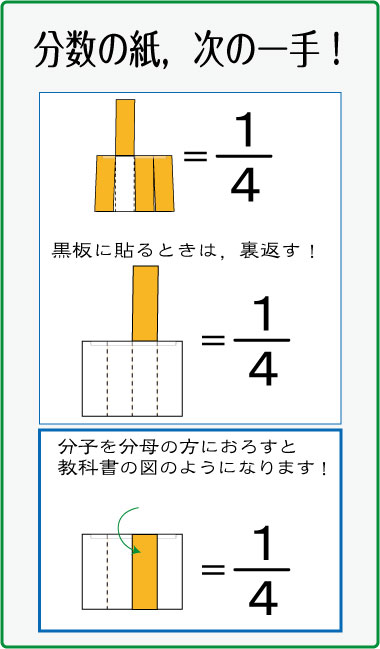



分数の紙 次の一手 さくら社
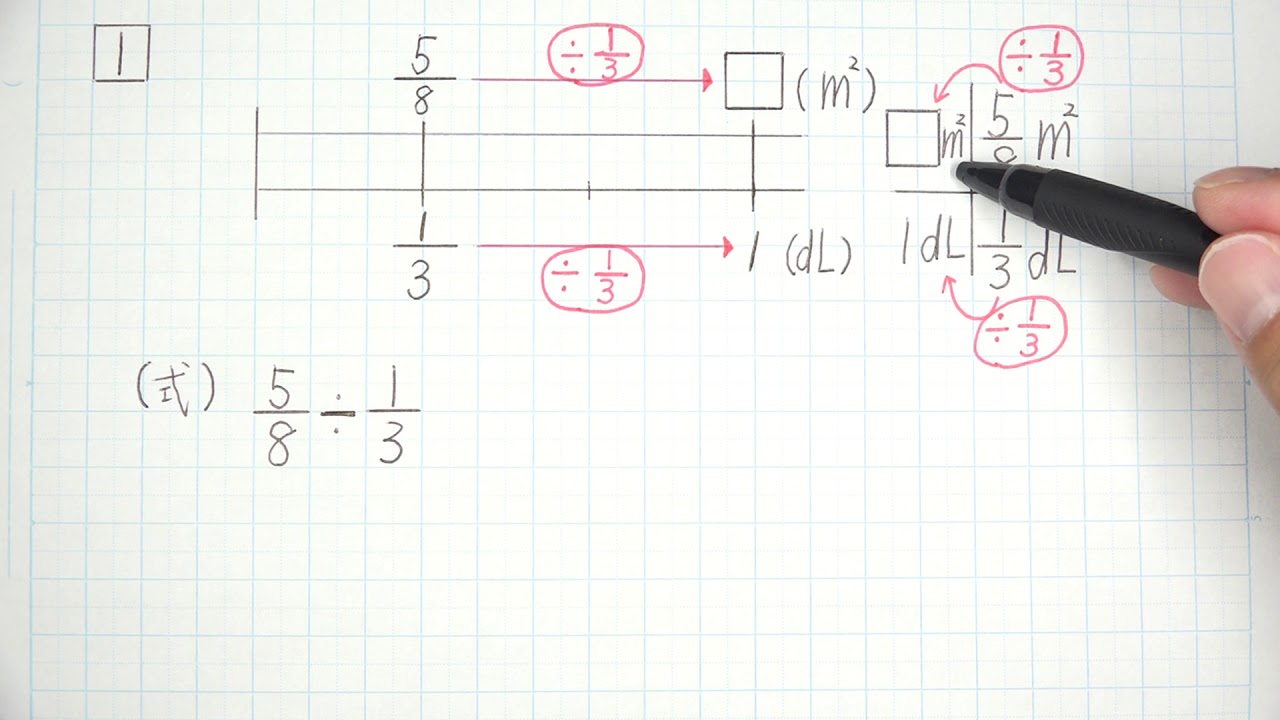



6年算数 分数のわり算 文章題 分数 分数 面積図を使って解説します Youtube




何で分数の割り算は逆数をかけるの 理由を説明できますか
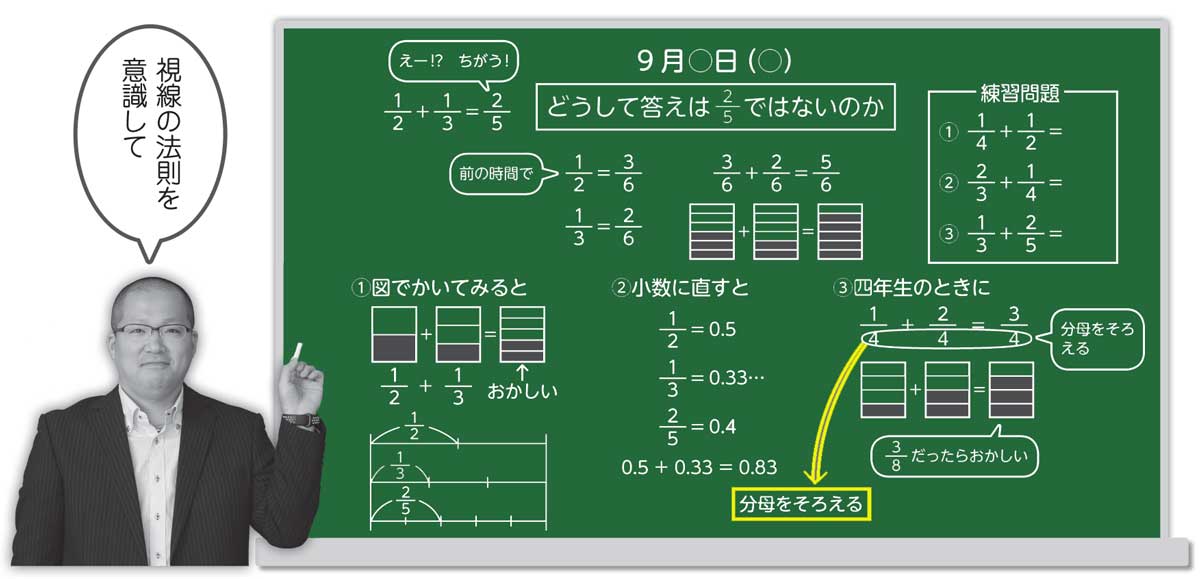



小学算数 構造的板書 の工夫とコツ 分数のたし算 ひき算 みんなの教育技術




ボード 子供に教えること のピン




6年算数分数 分数 わかる教え方
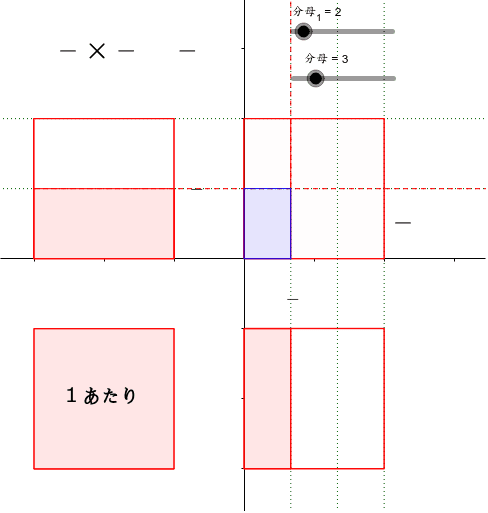



分数のかけわり図 かけ算 Geogebra



分数のかけ算 わり算2 シリウス 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材




面積図の縦と横は何を表すのか かけ算の順序の昔話



6年算数分数 分数 分数のわり算 教え方




4年生の後半になると 分数について これまでよりもくわしく習います 線分図の目盛りを読み取り 仮分数と帯分数で表そう 真分数 しんぶんすう 仮 分数 かぶんすう 帯分 学習ノート 学習 小学校 算数



1
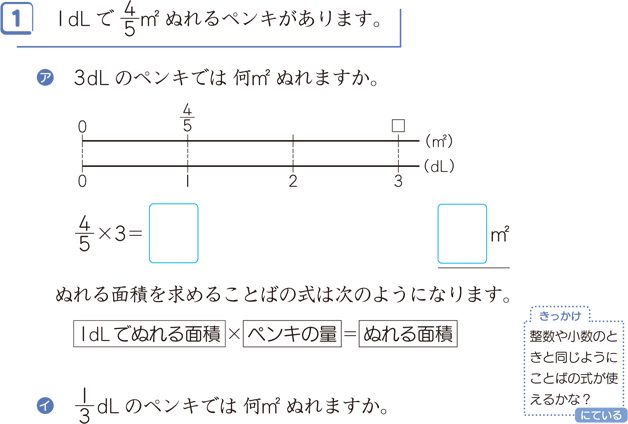



分数の乗法 算数用語集



Www Pref Miyagi Jp Uploaded Attachment Pdf




6年生算数 分数のわり算 面積図 分数のわり算の時 どうして後ろの分数の上下をひっくり返すのか お答えします Youtube



小4 分数の種類 仮分数 帯分数 と直すやり方の練習問題 そうちゃ式 分かりやすい図解算数 別館
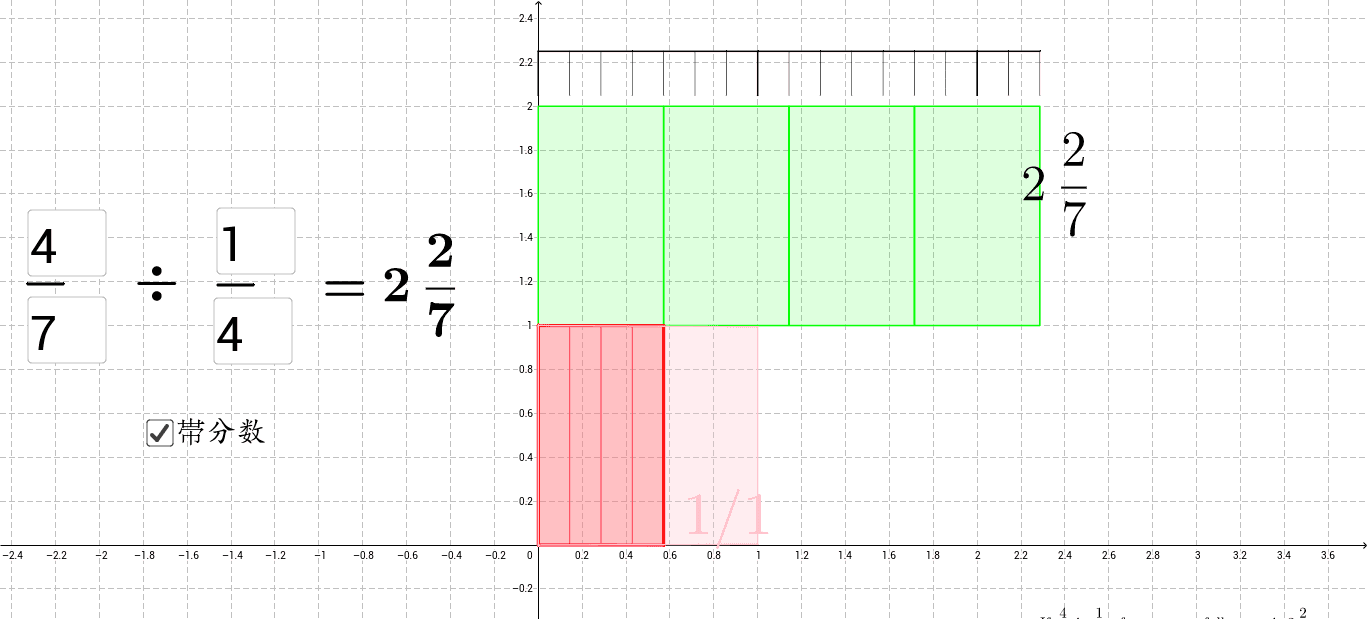



分数の割り算 Geogebra
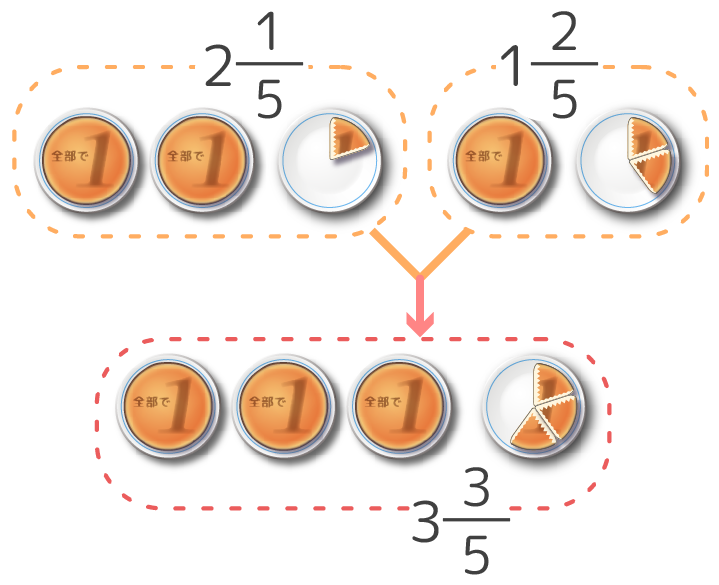



小学4年生 帯分数の足し算引き算 分数のくり上がり くり下がりも そうちゃ式 分かりやすい図解算数 別館
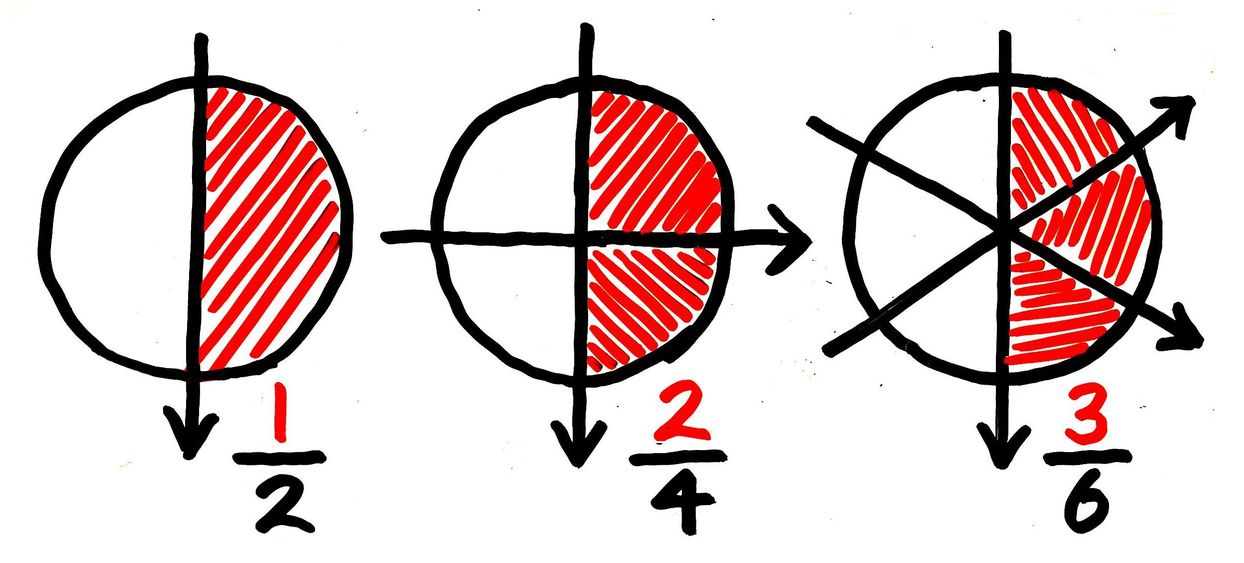



分数の総まとめ 苦手な人でも性質や計算方法を理解できます そうちゃ式 分かりやすい図解算数 別館



1
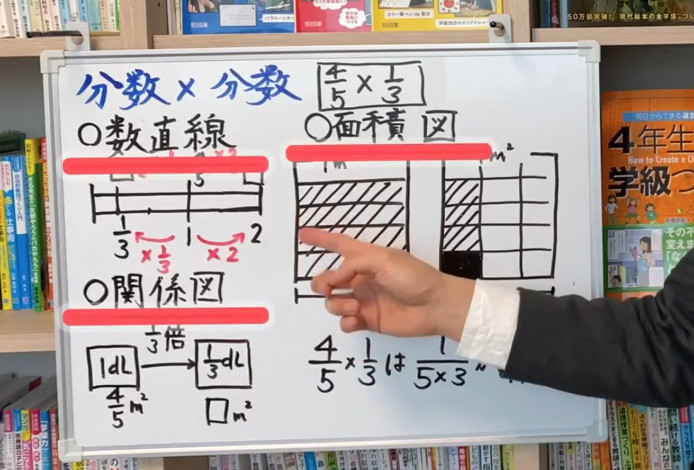



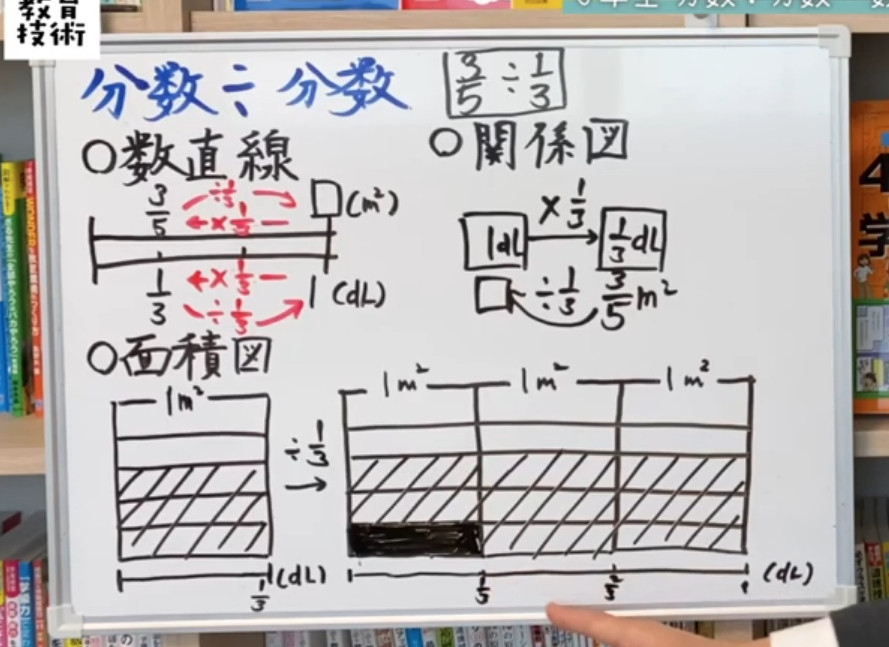
小6算数 分数 分数 数直線 面積図 関係図で攻略 動画 みんなの教育技術




1994 1108号 分数表示装置 Astamuse




分数のわり算 等分除 包含除 を数直線で かけ算の順序の昔話




復習プリントをやっているのですが 図がなぜこうなるのか全然分からないので Clear
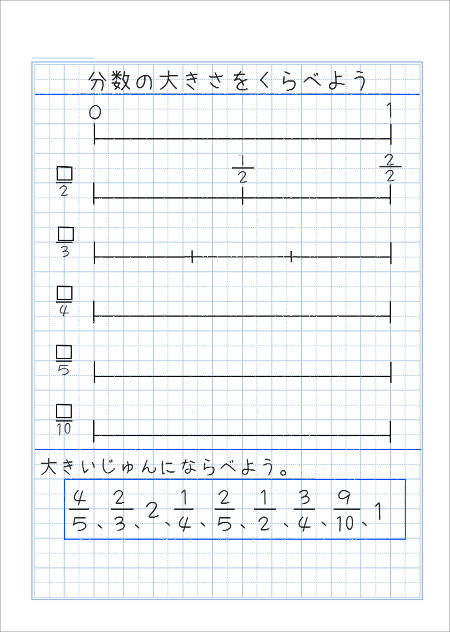



分数の大きさを比べよう 家庭学習レシピ
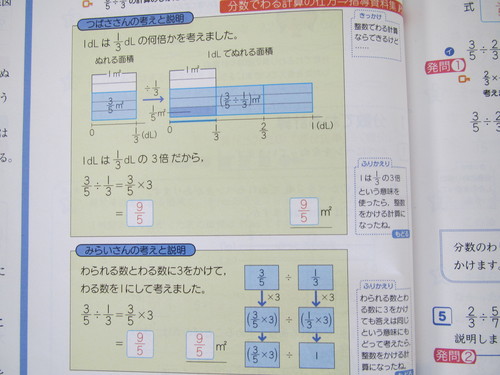



分数の授業18時間目 ワークブックを進める 石原清貴の算数教育ブログ



これで分母は足さないぞ 分数の足し算はこういうことだ 福岡 筑豊の家庭教師




研究 4ます関係面積図 1 授業がんばりmath




07 1723号 分数表示装置および分数表示プログラム Astamuse



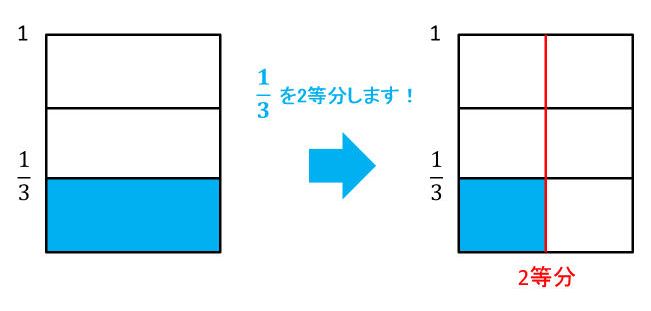
分数の理解が難しい児童へ 量イメージ から 帯分数 を色で描こう 図式
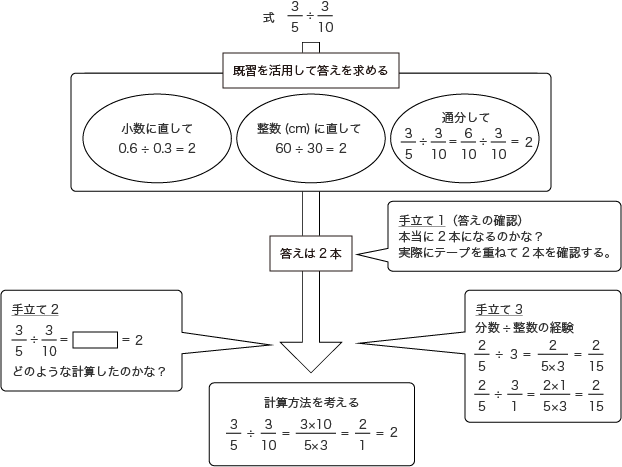



算数実践実例集 啓林館




研究 4ます関係面積図 2 授業がんばりmath




エジプト分数のかけ算part1 2倍表を使って 自然数 エジプト分数 を計算する ラッセル博士の数のお話 Note



3年算数分数その2わかる教え方



分数のわり算の仕組みを理解しよう 逆数をかけるのはどうして の謎に挑む 中学受験ナビ
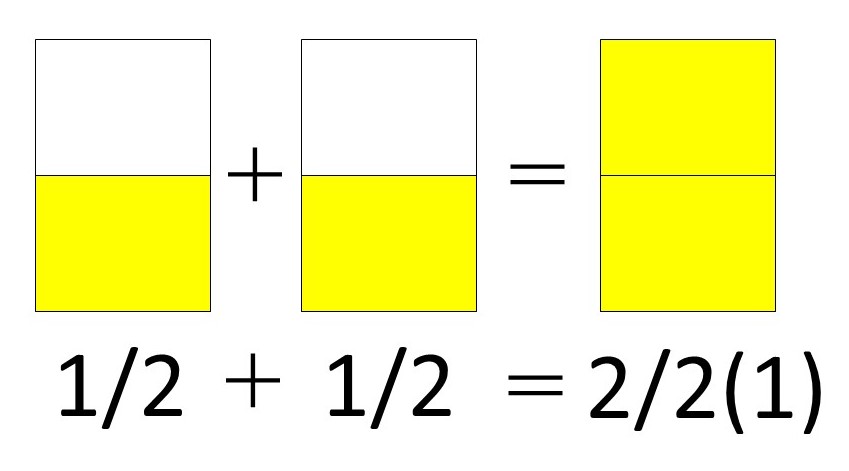



算数 この図を見ればもう間違えない 分数の足し算とかけ算 独断と偏見で楽しく教育を語る
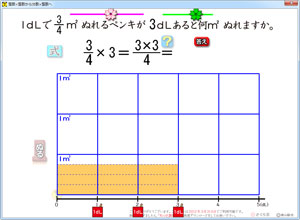



5年 分数のかけ算ソフト さくら社



分母をたす 間違いを防ぐ 分数たし算をイメージと色で描く 図式
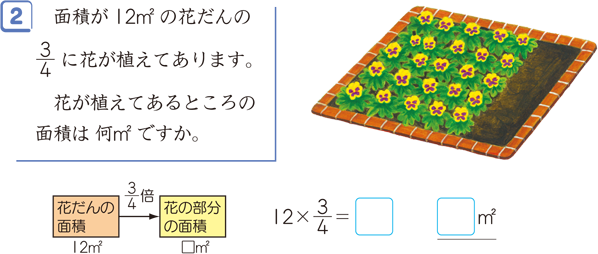



割合を表す分数 算数用語集




なぜ分数の割り算はひっくり返すのか 数学ギライも図に描けばすぐ理解できる Amazon De Bucher



分数のわり算の仕組みを理解しよう 逆数をかけるのはどうして の謎に挑む 中学受験ナビ



小6算数 分数 分数 数直線 面積図 関係図で攻略 動画 みんなの教育技術




1994 1108号 分数表示装置 Astamuse



1



分数の大きさのドリル 時間と分数のドリル



小6算数 分数 分数 数直線 面積図 関係図で攻略 動画 みんなの教育技術




小6算数 分数 分数 数直線 面積図 関係図で攻略 動画 みんなの教育技術




ヨドバシ Com つまずきをなくす小4算数文章題 わり算 線分図 小数や分数 計算のきまり 単行本 通販 全品無料配達




算数 分数の授業2分数の図を書く 授業力アップ 学級経営の話



分数が苦手 を克服するために 2 小 中学生向け補習塾 算数 数学 国語 ほめるん By じりつ堂



小6算数 分数 分数 数直線 面積図 関係図で攻略 動画 みんなの教育技術




大きさの等しい分数は 線ですぐわかる 算数嫌い0 ゼロ 先生のブログ




Amazon Co Jp 割合ポスターと分数の計算 分数の種類と計算ポスター 文房具 オフィス用品



図と色を使って 量イメージ から帯分数と仮分数へ変換しよう 図式



面積図 分数のかけ算 スクールプレゼンター教材共有サイト スクプレ道場



6年算数分数 分数 分数のわり算 教え方



分数ものさし 雲外蒼天



実践記録算数6年



Www Wakayama Wky Ed Jp Nagusa Wp Content Uploads Sites 52 18 03 F72f3031beb0fb0b1e49 1 Pdf



分数のわり算 小6 タイル図での指導



実践記録算数6年
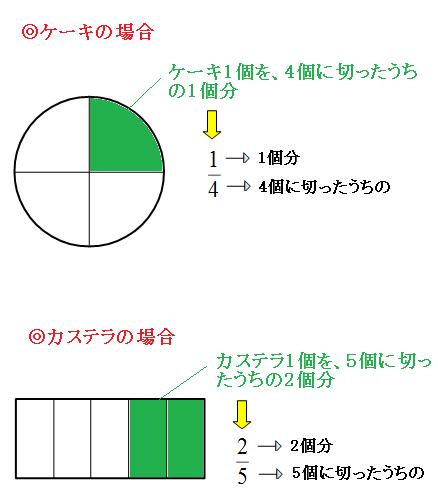



分数の基本をわかりやすく解説 分数とは何か を意識できれば超便利



3年算数分数その1教え方のポイント



図と色を使って 量イメージ から帯分数と仮分数へ変換しよう 図式




面積図 5分の2 分数 スクールプレゼンター教材共有サイト スクプレ道場



分数のかけ算 わり算1 シリウス 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材



6年算数分数 分数 教え方2



分数が苦手 を克服するために 3 小 中学生向け補習塾 算数 数学 国語 ほめるん By じりつ堂




算数マイスター 尾﨑正彦のブログ 3年 分数 の導入




分数のわり算 等分除 包含除 を数直線で かけ算の順序の昔話



面積図 算数用語集
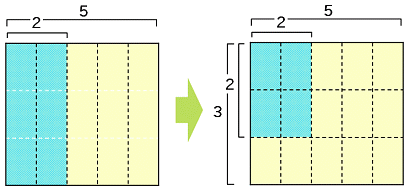



初等代数 分数を教える 掛け算 大人が学び直す数学
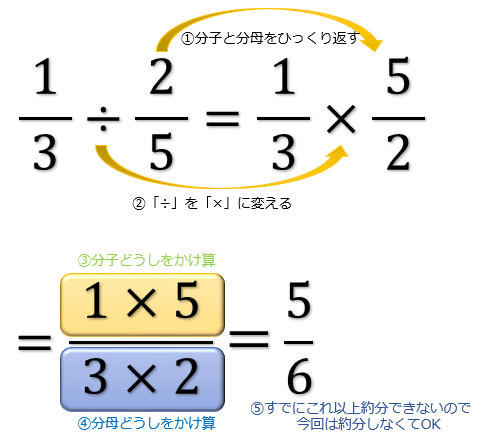



分数の割り算はなぜひっくり返してかけるのか その理由を説明する3つの教え方 逆数をかける理由 アタリマエ




File 分数説明図 Png Wikimedia Commons




6年算数 分数のかけ算 文章題 分数 分数の計算の仕方を考えよう Youtube
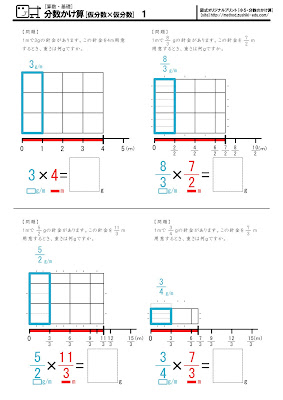



図で学ぶ算数基礎教材 分数のかけ算 導入 算数数学が苦手な子専門のプロ家庭教師みかん先生
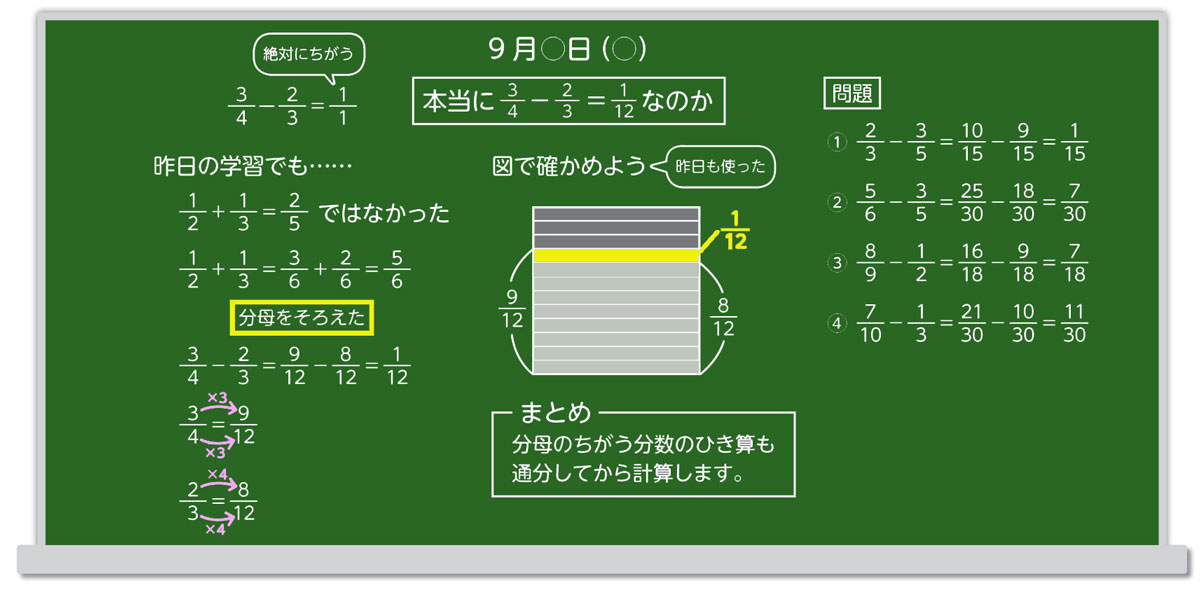



小学算数 構造的板書 の工夫とコツ 分数のたし算 ひき算 みんなの教育技術
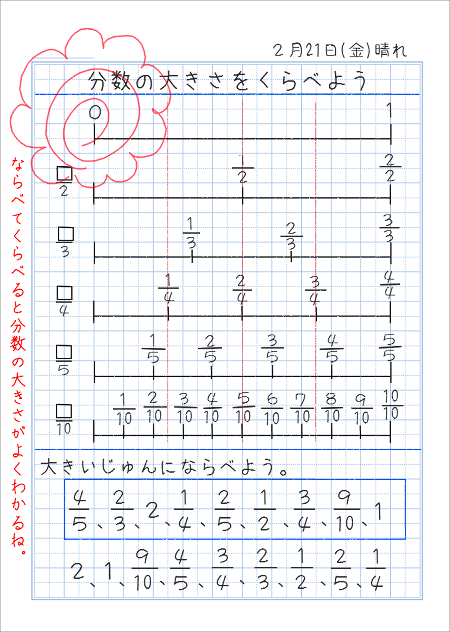



分数の大きさを比べよう 家庭学習レシピ




4年算数 分数 1 わかる教え方のポンイト
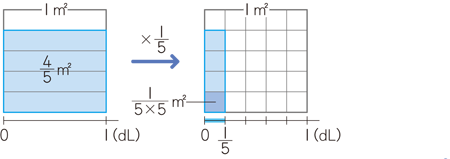



分数の乗法 算数用語集


